Точка дж: Что такое точка G и как её найти?

Posted on 28.02.202316.02.2023 by alexxlab

Музей эротики и секса «Точка G» в Москве

Музей эротики и секса «Точка G» в Москве

  • Реклама

    Реклама

    29309

  • mix» data-ping-position=»2″ data-featured-url=»https://kudago.com/msk/list/kuda-shodit-s-detmi-9/» data-item-url=»https://kudago.com/msk/list/kuda-shodit-s-detmi-9/» data-featured-path=»/msk/exhibitions/»>

    13

    49425

  • mix» data-ping-position=»2″ data-featured-url=»https://kudago.com/msk/list/organnaya-muzyika-v-moskve/» data-item-url=»https://kudago.com/msk/list/organnaya-muzyika-v-moskve/» data-featured-path=»/msk/exhibitions/»>

    133

    161063

  • mix» data-ping-position=»2″ data-featured-url=»https://kudago.com/msk/list/6-kontsertov-dlya-vlyublyonnyih-v/» data-item-url=»https://kudago.com/msk/list/6-kontsertov-dlya-vlyublyonnyih-v/» data-featured-path=»/msk/exhibitions/»>

    43

    99225

  • mix» data-ping-position=»3″ data-featured-url=»https://online.kudago.com/list/rasshiryaya-granitsyi-poznavatelnyie/» data-item-url=»https://online.kudago.com/list/rasshiryaya-granitsyi-poznavatelnyie/» data-featured-path=»/msk/exhibitions/»>

    3 6720

  • mix» data-ping-position=»3″ data-featured-url=»https://kudago.com/msk/list/vremya-tvorit-kursyi-i-master-/» data-item-url=»https://kudago.com/msk/list/vremya-tvorit-kursyi-i-master-/» data-featured-path=»/msk/exhibitions/»>

    11 10536

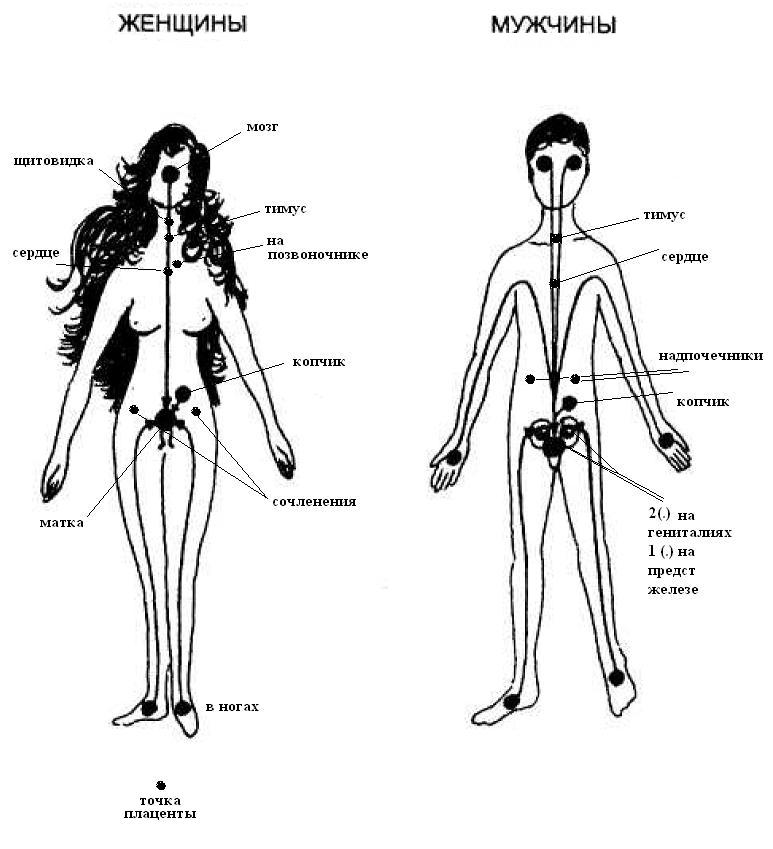
Музей «Точка G» — это не просто музей эротического искусства, он имеет и национальные особенности — «изюминки». Например, гигантский фаллос у входа, раскрашенный под гжель.

Много материалов посвящено сексу в СССР, которого, как известно, не было.

Так как музей создан для развлечения, то и все его экспонаты подобраны с юмором. Здесь много эротических пародий и насмешек. Экспонаты есть очень древние и современнейшие: старинные фаллоиммитаторы, статуэтки древних племён, различные знаменитости в откровенном изображении, «резиновые женщины», коллекция советских презервативов — резиновых изделий № 2. Много фотографий, картинок, книг и журналов на эротическую тему.

При покупке билета в музей, посетители могут заказать себе бесплатную программу экскурсий на сайте. В музее доступны программы: «Обзорная экскурсия», «Темная сторона эротики», «Современные секс-игрушки». Желающие могут заказать собственную откровенную фотосессию.

В музее эротики проходят различные выставки и презентации.

Кроме музея в «Точке G» есть еще и аттракционы для взрослых — «Лабиринт страха», «Зеркальный лабиринт» и бассейн шариков.

Необычные концерты в Соборе Петра и Павла.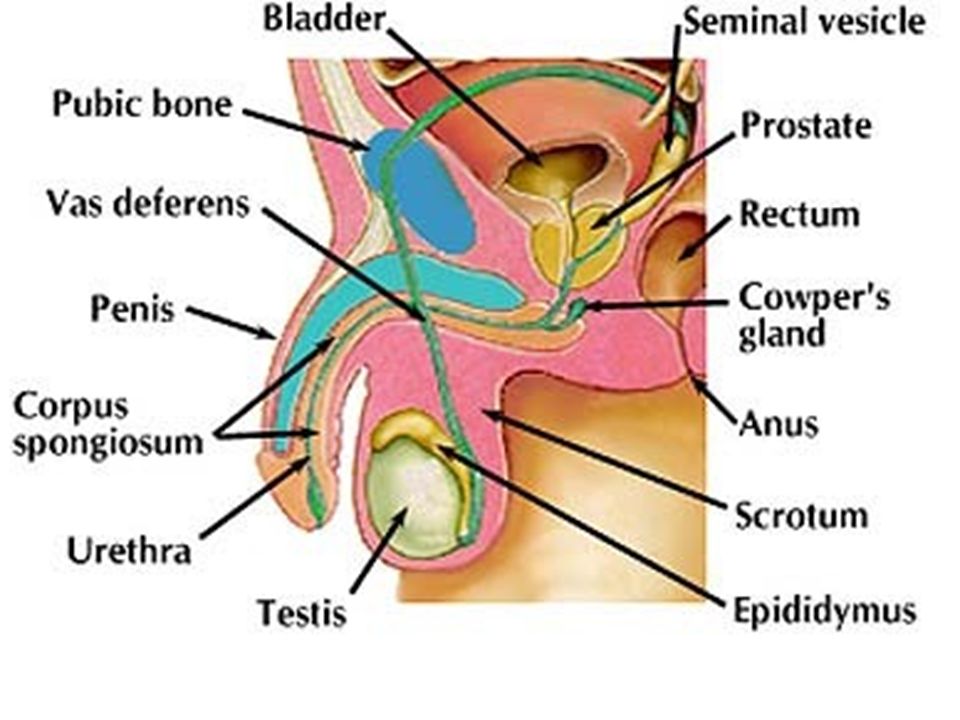 12+

Джаз, средневековая и классическая музыка на органе. Реклама. ИП Романенко Олег Иванович. ИНН 771471613250

Смотреть расписание

Если вы нашли опечатку или ошибку, выделите фрагмент текста, содержащий её, и нажмите Ctrl+↵

Расположение

Адрес Музея эротики и секса «Точка G»

ул. Новый Арбат, д. 15

Ближайшее метро

Арбатская

Дополнительная информация

Расписание работы

ежедневно 12:00–0:00

Телефон

Показать телефон

8 (800) 600-58-08

Пожалуйста, скажите владельцам места, что нашли его на KudaGo

Сайт

tochkag.net

Возрастное ограничение

18+

Выберите рассылку:

Нажимая на кнопку «Подписаться», вы соглашаетесь на передачу и обработку предоставленной персональной информации в соответствии с условиями Политики конфиденциальности.

Подписка оформлена

Спасибо!

Книга «Точка разрыва» Браун Дж

  • Книги
    • Художественная литература
    • Нехудожественная литература
    • Детская литература
    • Литература на иностранных языках
    • Путешествия. Хобби. Досуг
    • Книги по искусству
    • Биографии. Мемуары. Публицистика
    • Комиксы. Манга. Графические романы
    • Журналы
    • Печать по требованию
    • Книги с автографом
    • Книги в подарок
    • «Москва» рекомендует

    • Авторы • Серии • Издательства • Жанр

  • Электронные книги
    • Русская классика
    • Детективы
    • Экономика
    • Журналы
    • Пособия
    • История
    • Политика
    • Биографии и мемуары
    • Публицистика
  • Aудиокниги
    • Электронные аудиокниги
    • CD – диски
  • Коллекционные издания
    • Зарубежная проза и поэзия
    • Русская проза и поэзия
    • Детская литература
    • История
    • Искусство
    • Энциклопедии
    • Кулинария. Виноделие
    • Религия, теология
    • Все тематики
  • Антикварные книги
    • Детская литература
    • Собрания сочинений
    • Искусство
    • История России до 1917 года
    • Художественная литература. Зарубежная
    • Художественная литература. Русская
    • Все тематики
    • Предварительный заказ
    • Прием книг на комиссию
  • Подарки
    • Книги в подарок
    • Авторские работы
    • Бизнес-подарки
    • Литературные подарки
    • Миниатюрные издания
    • Подарки детям
    • Подарочные ручки
    • Открытки
    • Календари
    • Все тематики подарков
    • Подарочные сертификаты
    • Подарочные наборы
    • Идеи подарков
  • Канцтовары
    • Аксессуары делового человека
    • Необычная канцелярия
    • Бумажно-беловые принадлежности
    • Письменные принадлежности
    • Мелкоофисный товар
    • Для художников
  • Услуги
    • Бонусная программа
    • Подарочные сертификаты
    • Доставка по всему миру
    • Корпоративное обслуживание
    • Vip-обслуживание
    • Услуги антикварно-букинистического отдела
    • Подбор и оформление подарков
    • Изготовление эксклюзивных изданий
    • Формирование семейной библиотеки

Расширенный поиск

Браун Дж.

Формула скалярного произведения через компоненты вектора

Геометрическое определение скалярного произведения гласит, что скалярное произведение двух векторов $\vc{a}$ и $\vc{b}$ равно $$\vc{a} \cdot \vc{b} = \|\vc{a}\| \|\vc{b}\| \cos\тета,$$ где $\theta$ — угол между векторами $\vc{a}$ и $\vc{b}$. Хотя эта формула удобна для понимания свойств скалярного произведения, формула скалярного произведения в терминах компонентов вектора облегчила бы вычисление скалярного произведения между двумя заданными векторами.

В качестве первого шага рассмотрим скалярное произведение между стандартными единичными векторами, т. е. векторами $\vc{i}$, $\vc{j}$ и $\vc{k}$ длины один и параллельно осям координат.

Загрузка апплета

Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях: $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный) представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно.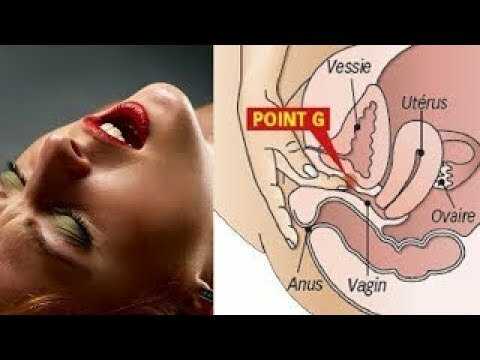 Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.

Дополнительная информация об апплете.

Поскольку стандартные единичные векторы ортогональны, мы немедленно заключаем, что скалярное произведение между парой различных стандартных единичных векторов равно нулю: \начать{выравнивать*} \vc{i} \cdot \vc{j} = \vc{i} \cdot \vc{k} = \vc{j} \cdot \vc{k}=0. \конец{выравнивание*} Скалярное произведение между единичным вектором и самим собой также просто вычислить. В этом случае угол равен нулю и $\cos\theta=1$. Учитывая, что все векторы имеют длину один, скалярные произведения равны \начать{выравнивать*} \vc{i} \cdot \vc{i} = \vc{j} \cdot \vc{j} = \vc{k} \cdot \vc{k}=1. \конец{выравнивание*}

Вторым шагом является вычисление скалярного произведения двух трехмерных векторов. \начать{выравнивать*} \vc{a} &= (a_1,a_2,a_3) = a_1\vc{i} + a_2\vc{j}+a_3\vc{k}\\ \vc{b} &= (b_1,b_2,b_3) = b_1\vc{i} + b_2\vc{j}+b_3\vc{k}. \конец{выравнивание*} Для этого мы просто утверждаем, что для любых трех векторов $\vc{a}$, $\vc{b}$ и $\vc{c}$ и любого скаляра $\lambda$ \начать{выравнивать*} (\lambda\vc{a}) \cdot \vc{b} &= \lambda(\vc{a}\cdot\vc{b}) = \vc{a} \cdot (\lambda\vc{b} )\\ (\vc{a}+\vc{b}) \cdot \vc{c} &= \vc{a} \cdot \vc{c} + \vc{b}\cdot \vc{c}. \конец{выравнивание*} (Эти свойства означают, что скалярное произведение является линейным.)

Учитывая эти свойства и тот факт, что скалярное произведение коммутативно, мы можем разложить скалярное произведение $\vc{a} \cdot \vc{b}$ по компонентам, \начать{выравнивать*} \vc{a} \cdot \vc{b} &= (a_1\vc{i} + a_2\vc{j}+a_3\vc{k}) \cdot (b_1\vc{i} + b_2\vc{j}+b_3\vc{k}) \\ &= a_1b_1 \vc{i} \cdot \vc{i} + a_2b_2\vc{j}\cdot\vc{j} + a_3b_3\vc{k}\cdot\vc{k} \\ &\quad + (a_1b_2+a_2b_1)\vc{i}\cdot\vc{j} + (a_1b_3+a_3b_1)\vc{i}\cdot\vc{k} \\ &\quad + (a_2b_3+a_3b_2)\vc{j}\cdot \vc{k}. \конец{выравнивание*} Поскольку мы знаем скалярное произведение единичных векторов, мы можем упростить формулу скалярного произведения до \начать{собирать} \vc{a} \cdot \vc{b} = a_1b_1+a_2b_2+a_3b_3.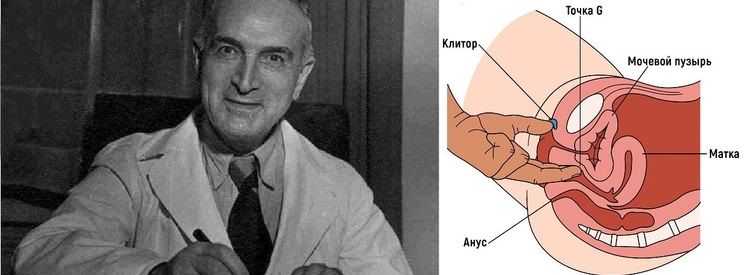 \метка{dot_product_formula_3d}\тег{1} \конец{собрать} 92$, еще проще. Данный \начать{выравнивать*} \vc{a} &= (a_1,a_2) = a_1\vc{i} + a_2\vc{j}\\ \vc{b} &= (b_1,b_2) = b_1\vc{i} + b_2\vc{j}, \конец{выравнивание*} мы можем использовать ту же формулу, но с $a_3=b_3=0$, \начать{собирать} \vc{a} \cdot \vc{b} = a_1b_1+a_2b_2 \label{dot_product_formula_2d}\tag{2}. \конец{собрать}

Вооружившись уравнениями \eqref{dot_product_formula_3d} и \eqref{dot_product_formula_2d}, вы можете быстро вычислить скалярные произведения, как показано в этих примерах.

Необычные типографские термины | Скараманга

Автор Саймон Лидбеттер

В этой статье мы рассмотрим некоторые менее известные типографские термины.