Квадрат Декарта
Пять шагов к колонизации Марса
Похоже на то, что довольно много людей хочет покинуть Землю. Что примечательно, Марс становится все более и более горячей темой для обсуждения, как с успехами и развитием SpaceX, так и в целом с актуализацией темы колонизации другой планеты. Кто, если не Марс? В связи с Красной планетой разрабатываются самые любопытные темы и сценарии, от строительства подземных баз до полного облагораживания планеты, превращения ее во вторую Землю. Бывший астронавт Джефф Хоффман, к примеру, планирует снабдить Марс кислородом.
Однажды это случится. NASA готовится к производству своей новой тяжелой ракеты, Space Launch System (SLS), которая сможет отправить людей за пределы земной орбиты; авось и нелепое шоу Mars One как-нибудь выкрутится и все же начнет заниматься приличными делами; основные надежды, конечно, возлагают на SpaceX.
Мы уже пришли к выводу о том, что человеческая цивилизация однозначно должна и заселит Марс.
 А если они захотят иметь здоровых марсианских детей, космическая радиация также может повредить сперму и яйцеклетки.
Безопасная высадка на Марс тоже представляет собой проблему. NASA использовало инновационный «небесный кран», чтобы посадить однотонный марсоход «Кьюриосити» на поверхность в 2012 году. Капсула «Орион» весит почти 10 тонн, не считая посадочную ракету или сервисный модуль. Агентство в настоящее время разрабатывает гигантские надувные тепловые щиты, которые замедлят космический аппарат во время приближения к Марсу, и сделают посадку крупного судна осуществимой.
Хорошая новость в том, что добраться до Марса за один присест — это, по сути, инженерская задача, но существуют дела и посложнее. Джефф Хоффман указывает на то, что вся затея будет очень дорогой. «Какие финансы потребуются для освоения людьми Марса, трудно даже предположить», — отмечает он. Десятки миллиардов долларов, не меньше. Хоффман предполагает, что новое поколение предприимчивых миллиардеров, заинтересованных в освоении космоса, может стать частью нового, общественного решения.
А если они захотят иметь здоровых марсианских детей, космическая радиация также может повредить сперму и яйцеклетки.
Безопасная высадка на Марс тоже представляет собой проблему. NASA использовало инновационный «небесный кран», чтобы посадить однотонный марсоход «Кьюриосити» на поверхность в 2012 году. Капсула «Орион» весит почти 10 тонн, не считая посадочную ракету или сервисный модуль. Агентство в настоящее время разрабатывает гигантские надувные тепловые щиты, которые замедлят космический аппарат во время приближения к Марсу, и сделают посадку крупного судна осуществимой.
Хорошая новость в том, что добраться до Марса за один присест — это, по сути, инженерская задача, но существуют дела и посложнее. Джефф Хоффман указывает на то, что вся затея будет очень дорогой. «Какие финансы потребуются для освоения людьми Марса, трудно даже предположить», — отмечает он. Десятки миллиардов долларов, не меньше. Хоффман предполагает, что новое поколение предприимчивых миллиардеров, заинтересованных в освоении космоса, может стать частью нового, общественного решения.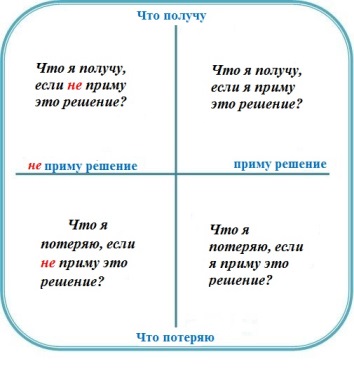
 Извлечение воды из мочи и пота уже показало себя эффективной системой утилизации — проверенной на Международной космической станции. Это поможет поначалу, но будет недостаточно для поддержания сообщества, поэтому местный источник пресной воды будет крайне необходим.
Производство продуктов питания на Марсе может быть намного сложнее. Некоммерческая организация Mars Society экспериментировала с выращиванием пищи на изолированной пустынной научно-исследовательской станции в штате Юта. «Нам удалось сделать некоторую интересную биологию, но до аппетитной биологии мы не дошли», — говорит программный инженер и энтузиаст Марса Дигби Тарвин о своем последнем пребывании на станции 10 лет назад.
Тарвин собирается вернуться к научно-исследовательской станции в Юте и говорит, что с тех пор был достигнут существенный прогресс. «Люди вырастили съедобную зелень, но этого пока недостаточно, чтобы мы начали жить на том, что производим, — говорит он. — Один из исследовательских проектов предполагает возможное использование местных пород в качестве питательного субстрата с добавлением достаточных минералов и удобрений».
Извлечение воды из мочи и пота уже показало себя эффективной системой утилизации — проверенной на Международной космической станции. Это поможет поначалу, но будет недостаточно для поддержания сообщества, поэтому местный источник пресной воды будет крайне необходим.
Производство продуктов питания на Марсе может быть намного сложнее. Некоммерческая организация Mars Society экспериментировала с выращиванием пищи на изолированной пустынной научно-исследовательской станции в штате Юта. «Нам удалось сделать некоторую интересную биологию, но до аппетитной биологии мы не дошли», — говорит программный инженер и энтузиаст Марса Дигби Тарвин о своем последнем пребывании на станции 10 лет назад.
Тарвин собирается вернуться к научно-исследовательской станции в Юте и говорит, что с тех пор был достигнут существенный прогресс. «Люди вырастили съедобную зелень, но этого пока недостаточно, чтобы мы начали жить на том, что производим, — говорит он. — Один из исследовательских проектов предполагает возможное использование местных пород в качестве питательного субстрата с добавлением достаточных минералов и удобрений».

 Поверхность можно было бы пробурить с образованием пещер, породы извлечь для дальнейшего использования в качестве строительных материалов — так же, как мы строим дома из камня на Земле. Также может быть возможно извлечь полезные ископаемые для разработки металлов или стекла.
Роберт Зубин, президент Mars Society, является одним из ведущих сторонников терраформирования Марса — превращения планеты из безвоздушного бесплодного мира в зеленый и богатый кислородом, с полностью функционирующей экосистемой.
Существует, однако, основная проблема в попытке наполнить Марс пригодной для дыхания атмосферой. Атмосфера Земли содержится в магнитном пузыре, известном как магнитосфера, порожденном нашим магнитным полем. У Марса такого поля нет, и любая атмосфера, которая когда-либо на нем была, скорее всего была унесена потоком заряженных частиц, или солнечным ветром, несущимся от Солнца.
История прошлого марсианской атмосферы в настоящее время исследуется миссией Maven, но даже если мы воссоздадим на Красной планете этот тонкий пузырь из пригодной для дыхания воздуха, скорее всего его ждет судьба прошлой атмосферы.
Поверхность можно было бы пробурить с образованием пещер, породы извлечь для дальнейшего использования в качестве строительных материалов — так же, как мы строим дома из камня на Земле. Также может быть возможно извлечь полезные ископаемые для разработки металлов или стекла.
Роберт Зубин, президент Mars Society, является одним из ведущих сторонников терраформирования Марса — превращения планеты из безвоздушного бесплодного мира в зеленый и богатый кислородом, с полностью функционирующей экосистемой.
Существует, однако, основная проблема в попытке наполнить Марс пригодной для дыхания атмосферой. Атмосфера Земли содержится в магнитном пузыре, известном как магнитосфера, порожденном нашим магнитным полем. У Марса такого поля нет, и любая атмосфера, которая когда-либо на нем была, скорее всего была унесена потоком заряженных частиц, или солнечным ветром, несущимся от Солнца.
История прошлого марсианской атмосферы в настоящее время исследуется миссией Maven, но даже если мы воссоздадим на Красной планете этот тонкий пузырь из пригодной для дыхания воздуха, скорее всего его ждет судьба прошлой атмосферы.
 — Реальное общество с реальными людьми, живущими настоящей жизнью, с детьми, со школами, с оркестрами и так далее».
Ребенок, рожденный по красным небом Марса, наверняка будет иметь отличное от земного мировоззрения и, возможно, никогда не вернется на родную планету. Каждый шаг к установлению человеческой цивилизации на Марсе вполне возможен. Остается один вопрос: а вы пойдете на это? Марс — холодное, безвоздушное, жестокое и красное место. Простая задача выживания на нем станет ежедневным вызовом.
— Реальное общество с реальными людьми, живущими настоящей жизнью, с детьми, со школами, с оркестрами и так далее».
Ребенок, рожденный по красным небом Марса, наверняка будет иметь отличное от земного мировоззрения и, возможно, никогда не вернется на родную планету. Каждый шаг к установлению человеческой цивилизации на Марсе вполне возможен. Остается один вопрос: а вы пойдете на это? Марс — холодное, безвоздушное, жестокое и красное место. Простая задача выживания на нем станет ежедневным вызовом.Как научиться принимать решения с помощью квадрата Декарта
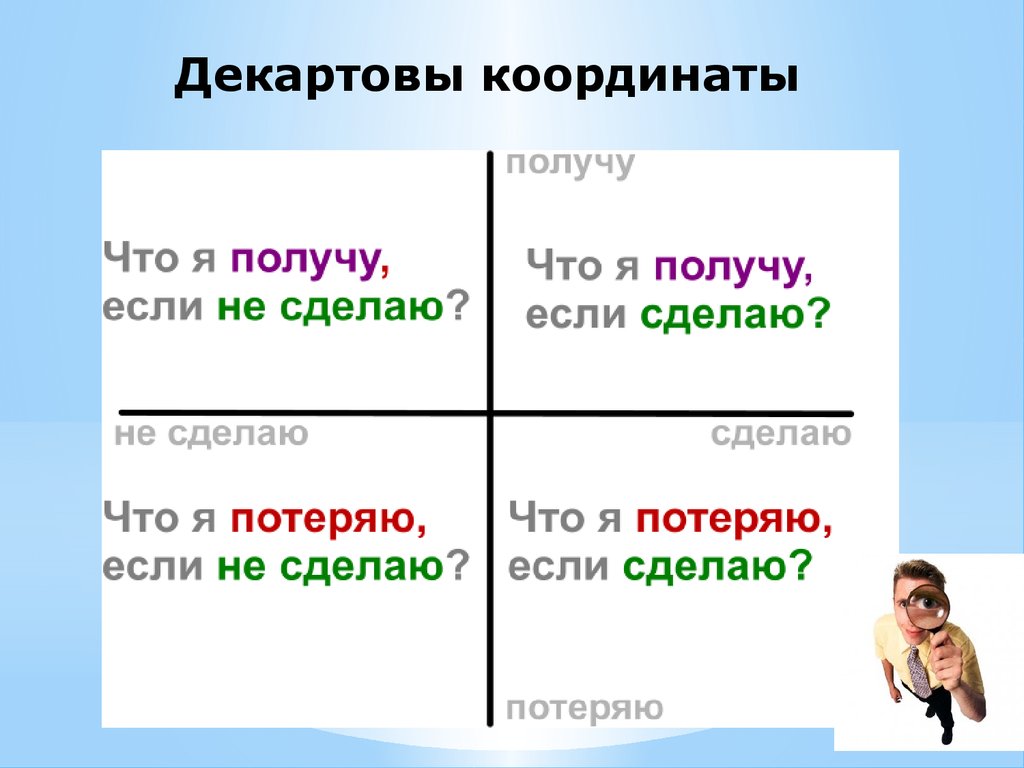
Вся наша жизнь — это ежедневное принятие решений. Сложных и не очень, судьбоносных и тривиальных. Мы обычно восхищаемся решительными людьми и избегаем брать в команду нерешительных. Умение брать на себя ответственность и принимать решения — это навык, которому можно и нужно научиться. Еще в 17 веке французский математик и философ Рене Декарт предложил способ, помогающий принимать решения в любых ситуациях. Квадрат Декарта — простая, но действенная методика, которая удивит и вас и ваших учеников. Давайте разберемся с ней вместе, и вы сможете передать своим студентам еще одно важное умение.
Давайте разберемся с ней вместе, и вы сможете передать своим студентам еще одно важное умение.
В основе метода Декарта лежат
четыре вопроса:- Что я получу, если это произойдет?
- Что я получу, если этого не произойдет?
- Что я потеряю, если это произойдет?
- Что я потеряю, если этого не произойдет?
Или так:
https://4brain.ru/Нужно всего лишь подставить свою конкретную ситуацию в эту схему и дать исчерпывающее количество как можно более точных ответов. Ответы должны быть детальными, вдумчивыми, взвешенными.
Квадрат решений Декарта позволяет посмотреть на ситуацию или проблему со всех сторон, не фокусируясь только на “плюсах” или “минусах”. Благодаря этой технике можно избежать однобокого взгляда на решение и проанализировать все необходимые аспекты.
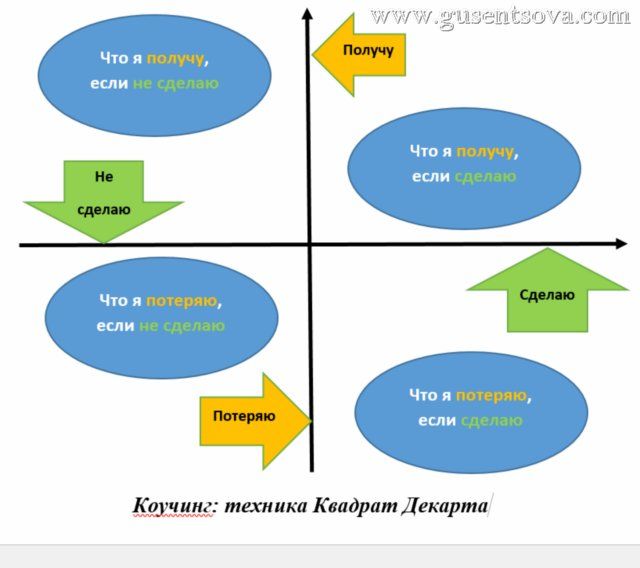
Лучше всего пользоваться этим методом визуально. Для этого нужно разделить лист бумаги на четыре части и письменно ответить на 4 вопроса, которые мы упоминали выше. Здесь скрыт чисто психологический момент. Наше сознание устроено так, что мы часто непроизвольно игнорируем частицу “нет” тогда, когда нам это почему-то выгодно. В таком случае смысл некоторых квадратов просто теряется.
Здесь скрыт чисто психологический момент. Наше сознание устроено так, что мы часто непроизвольно игнорируем частицу “нет” тогда, когда нам это почему-то выгодно. В таком случае смысл некоторых квадратов просто теряется.
Но если наши ответы на вопросы Квадрата Декарта предельно честны и прозрачны, правильное решение будет на поверхности, и его можно будет легко увидеть.
Квадрат для принятий решений прекрасен тем, что он применим в любых сферах жизни: от бытовых неурядиц до жизненно важных проблем. Техника Декарта проста и вместе с тем универсальна.
Посмотрим, как Квадрат Декарта работает на практике. Например, вы решили пройти курс повышения квалификации на Coursera, но сомневаетесь, нужно ли вам это сейчас, хватит ли у вас энергии и времени делать это. Рисуем Квадрат Декарта и начинаем откровенно отвечать на вопросы:
— если я всё-таки займусь этим, то:
спустя какое-то время буду лучшим специалистом в своей области, чем я есть сейчас, смогу сменить работу на более высокооплачиваемую и т. п.
п.
— если я НЕ буду этого делать, то:
у меня будет сейчас больше свободного времени, я буду проводить достаточно свободного времени за любимыми занятиями, читать много книг, вдоволь смотреть любимые фильмы;
— если я буду проходить курс, я НЕ:
смогу проводить много времени с семьей и смотреть любимый сериал;
— если я НЕ займусь курсом, я:
не смогу претендовать на продвижение на работе, я буду не в курсе новых тенденций.
Прописав все ответы и имея перед глазами все варианты развития событий в зависимости от принятого решения, легко сопоставить риски и последствия, выгоду и возможные потери и принять осознанное решение.
500 Внутренняя ошибка сервера в CatLab Joyal
Пропустить навигационные ссылки | Домашняя страница | Все страницы |
Пожалуйста, сообщите об этом на nForum в категории nLab Technical Matters . Пожалуйста, предоставьте как можно более точную информацию о том, что вызвало ошибку.
Домашняя страница nLab
Вот ошибка:
Отсутствует шаблон /errors/404.rhmtl в пути просмотра /home/nlab/www/nlab/app/views
И вот трассировка исключения:
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_view/paths.rb:74:in `find_template' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_view/base.rb:264:in `render' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_view/base.rb:348:in `_render_with_layout' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_view/base.rb:262:in `render' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:1252:in `render_for_file' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:936: в `рендеринге' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:51:in `блок в render_with_benchmark' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `блок в мс' /usr/share/ruby/benchmark.rb:308:в `реальном времени' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `мс' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:51:in `render_with_benchmark' /home/nlab/www/nlab/app/controllers/wiki_controller.rb:303:в `опубликовано' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:1333:in `perform_action' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:617:in `call_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:206:in `блокировать в around_proc' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.
rb:615:in `call_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:189: в `вызове' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:91:in `фильтр' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:66:in `блок в caches_action' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.
rb:635:in `run_before_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:610:in `perform_action_with_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `заблокировать в Perform_action_with_benchmark' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `блок в мс' /usr/share/ruby/benchmark.rb:308:в `реальном времени' /home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `мс' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `perform_action_with_benchmark' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/rescue.rb:160:in `perform_action_with_rescue' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/flash.rb:151:in `perform_action_with_flash' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.
rb:532:в `процессе' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:606:in `process_with_filters' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:391: в `процессе' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:386:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/routing/route_set.rb:438:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:87:в `dispatch' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:121:in `_call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:130:in `блок в build_middleware_stack' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/string_coercion.rb:29: в `вызове' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/head.rb:12:in `call' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/method_override.rb:24:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/params_parser.
rb:15:in `call' /home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/metal.rb:47:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/session/abstract_store.rb:177:in `call' /home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:29:in `заблокировать вызов' /home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/query_cache.rb:34:в `кеше' /home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:9:в `кеше' /home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:28:in `call' /home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/connection_pool.rb:361:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/failsafe.rb:26:in `call' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/lock.rb:18:in `call' /home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:106:in `call' /home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/static.
rb:31:in `call' /home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/log_tailer.rb:17:in `call' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:634:in `process_client' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:739: в `worker_loop' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:547:in spawn_missing_workers /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:143:в `start' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/bin/unicorn_rails:209:in `
' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/bin/unicorn_rails:25:in `load' /home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/bin/unicorn_rails:25:in ` ' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli/exec.rb:58:in `load' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli/exec.rb:58:in `kernel_load' /usr/share/gems/gems/bundler-2. 2.33/lib/bundler/cli/exec.rb:23:in `run' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:479: в `exec' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/command.rb:27:in `run' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/invocation.rb:127:in `invoke_command' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor.rb:392:in `dispatch' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:31:in `dispatch' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/base.rb:485:в `start' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:25:в `start' /usr/share/gems/gems/bundler-2.2.33/libexec/bundle:49:in `заблокировать в
' /usr/share/gems/gems/bundler-2.2.33/lib/bundler/friendly_errors.rb:103:in `with_friendly_errors' /usr/share/gems/gems/bundler-2.2.33/libexec/bundle:37:in ` ' /usr/bin/bundle:23:in `загрузить' /usr/bin/bundle:23:in ` '
теория категорий — «магическая диаграмма» является декартовой
Задавать вопрос
спросил
Изменено 1 месяц назад
Просмотрено 6к раз
$\begingroup$
Я пытаюсь решить упражнение из конспекта лекций Вакиля по алгебраической геометрии, а именно хочу показать, что $\require{AMScd}$ \начать{CD} X_1\times_Y X_2 @>>> X_1\times_Z X_2\\ @В В В @ВВ В\\ Y @>>> Y \times_Z Y \конец{CD}
— это декартова диаграмма. Кажется, я понял, откуда берутся карты: нижняя карта — это диагональ, индуцированная универсальным свойством $Y \times_Z Y$, верхняя карта — универсальным свойством $X_1\times_Z X_2$ (это является одним из предыдущих упражнений в заметках Вакила), карта справа также происходит из универсального свойства $Y \times_Z Y$, поскольку у нас есть две карты из $X_1\times_Z X_2$ в $Y$, композиция которых с $Y \rightarrow Z$ совпадает, и, наконец, карта в левой части является либо композицией $X_1\times_Y X_2 \rightarrow X_i \rightarrow Y$. На данный момент я даже не понимаю, почему эта диаграмма должна быть коммутативной.
Кажется, я понял, откуда берутся карты: нижняя карта — это диагональ, индуцированная универсальным свойством $Y \times_Z Y$, верхняя карта — универсальным свойством $X_1\times_Z X_2$ (это является одним из предыдущих упражнений в заметках Вакила), карта справа также происходит из универсального свойства $Y \times_Z Y$, поскольку у нас есть две карты из $X_1\times_Z X_2$ в $Y$, композиция которых с $Y \rightarrow Z$ совпадает, и, наконец, карта в левой части является либо композицией $X_1\times_Y X_2 \rightarrow X_i \rightarrow Y$. На данный момент я даже не понимаю, почему эта диаграмма должна быть коммутативной.
Но даже если отбросить проблему коммутативности, учитывая некоторое $T$ вместо $X_1\times_Y X_2$, делающее приведенную выше диаграмму коммутирующей, я понятия не имею, как получить каноническое отображение $T \rightarrow X_1\times_Y X_2$.
Я мог бы решить все остальные задачи в этом разделе его заметок, но эта ускользает от меня. Мы будем очень признательны за любую помощь или решение (желательно просто с использованием предоставленных нам универсальных свойств).
- теория категорий
- пределы-копределы
$\endgroup$
$\begingroup$
Во-первых, почему диаграмма коммутативна: у вас есть следующая коммутативная диаграмма:
Оно коммутативно именно потому, что именно так мы определили отображение $X_1 \times_Y X_2 \to X_1 \times_Z X_2$. Нижний правый квадрат используется для определения $Y \to Y \times_Z Y$.
Теперь ваша диаграмма является коммутативной, если две карты $X_1 \times_Y X_2 \to Y \times_Z Y$ равны, если и только если карты каждой компоненты равны.
- Красный путь используется для определения (первого компонента) карты, которая факторизуется через $X_1 \times_Y X_2 \to X_1 \times_Z X_2 \to Y \times_Z Y$
- Синий путь используется для определения (первого компонента) карты, которая факторизуется через $X_1 \times_Y X_2 \to Y \to Y \times_Z Y$.
Как видите, они равны. Следовательно, магическая диаграмма коммутирует.
Следовательно, магическая диаграмма коммутирует.
Теперь универсальное свойство. Предположим, вам даны $T \to X_1 \times_Z X_2$ и $T \to Y$, так что два отображения $T \to Y \times_Z Y$ равны. Другими словами, вам даны отображения $T \to X_1$, $T \to X_2$ и $T \to Y$, такие, что два отображения $T \to X_i \to Z$ равны, а отображения синий путь и красный путь равны (где $T$ находится в позиции $X_1 \times_Y X_2$). Как видите, это то же самое, что дать два отображения $T \to X_i$, такие что $T \to X_i \to Y$ равны, потому что тогда равенство отображений в $Z$ является следствие того, что отображения в $Y$ равны. Итак, существует уникальная карта $T \to X_1 \times_Y X_2$, делающая все коммутирующими.
Учитывая, что Вакиль вводит лемму Йонеды после этого упражнения, я не осмелился привести доказательство с ее помощью. Но по лемме Йонеды вы можете просто рассмотреть случай множеств; в уравнениях, которые вы напишете, вы придете к тому же заключению — что предоставление карт, которые заставляют все коммутировать, даст вам избыточное условие, что образы в $Z$ одинаковы, и что расслоенное произведение все дело в расслоенном произведении над $Y$.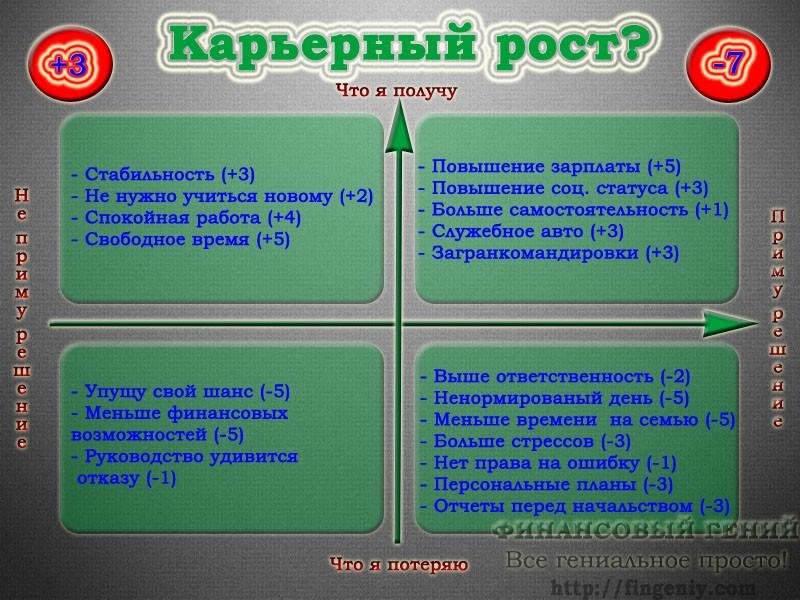
$\endgroup$
10
$\begingroup$
Вот несколько советов. Прежде всего, когда что-то кажется совсем неясным, полезно рассмотреть категорию множеств. В этом случае множество $X_1 \times_Y X_2$ состоит из пар $(x_1, x_2)$, имеющих одинаковый образ в $Y,$, и композиции $X_1 \times_Y X_2 \to Y \to Y \times_Z Y$ отправляет $(x_1, x_2) \mapsto (y, y),$, где $y$ — общий образ $x_1$ и $x_2.$ С другой стороны, $X_1 \times_Z X_2$ состоит из пар $(x_1 , x_2)$, где $x_i$ имеют одинаковые изображения в $Z$ . В частности, это множество естественно содержит $X_1 \times_Y X_2,$, а составное $X_1 \times_Y X_2 \to X_1 \times_Z X_2 \to Y \times_Z Y$ есть $(x_1, x_2) \mapsto (y, y)$ — так же, как прежде! Итак, у нас есть коммутативность на уровне множеств, и то же самое «должно работать» и на уровне схем. Просто перефразируйте, используя функтор точек или универсальных свойств (правда, это немного громоздко).
Но вы хотите показать, что квадрат декартов. Опять же, я уверен, что это можно сделать, используя аргументы универсальных свойств (или функтор точек, возможно, проще), но иногда может быть проще, так сказать, просто приступить к делу. Вспоминая определение расслоенного произведения, более или менее очевидно, что его можно свести к аффинному случаю. Итак, пусть $A, B, C_1, C_2$ — кольца. Вы хотите показать, что $B \otimes_{B \otimes_A B} (C_1 \otimes_A C_2) \ приблизительно C_1 \otimes_B C_2.$ Опять же, есть элегантный способ и способ грубой силы. Для последнего вы заметите, что левая часть порождается тензорами вида $b \otimes (c_1 \otimes c_2).$ Но вы можете использовать структуру $B \otimes_A B$-алгебры следующим образом: $b \otimes (c_1 \otimes c_2) = (b \otimes 1) [1 \otimes (c_1 \otimes c_2)] = 1 \otimes (b \otimes 1)(c_1 \otimes c_2) = 1 \otimes (bc_1 \otimes c_2) .$ Используя вместо этого $1 \otimes b$, вы получите $c_1 \otimes bc_2.$ В любом случае теперь у вас есть очевидная карта генераторов, и вам нужно только показать, что отношения соответствуют друг другу.
Это самое главное. Как я уже говорил несколько раз, аргумент можно сократить во многих моментах, заменив явную проверку с использованием конструкции аргументом универсальных свойств, и это, вероятно, правильный путь. Приведенная выше явная работа может помочь вам найти элегантное доказательство.
$\endgroup$
$\begingroup$
Я хочу добавить очень быстрое доказательство к уже существующим ответам. Предположим, что категория $\mathcal C$ имеет конечные пределы. Нам нравится показывать, что каждый магический квадрат является откатом в $\mathcal C$.
Вложение Yoenda является полностью точным и, таким образом, отражает ограничения. Следовательно, если мы можем показать, что каждый магический квадрат является обратным образом в $Pr(\mathcal C)$ после применения к нему вложения Йонеды $y:\mathcal C\to Pr(\mathcal C)$, то мы закончили . Поскольку вложение Йонеды также сохраняет все пределы, мы видим, что если мы можем показать теорему о магических квадратах для категории $Pr(\mathcal C)$, то она применима, в частности, к тем, которые мы получили из $\mathcal C$ через вложение Йонеды.
 rhmtl в пути просмотра /home/nlab/www/nlab/app/views
rhmtl в пути просмотра /home/nlab/www/nlab/app/views  rb:17:in `мс'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:51:in `render_with_benchmark'
/home/nlab/www/nlab/app/controllers/wiki_controller.rb:303:в `опубликовано'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:1333:in `perform_action'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:617:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:206:in `блокировать в around_proc'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.
rb:17:in `мс'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:51:in `render_with_benchmark'
/home/nlab/www/nlab/app/controllers/wiki_controller.rb:303:в `опубликовано'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:1333:in `perform_action'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:617:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:206:in `блокировать в around_proc'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters. rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:189: в `вызове'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:91:in `фильтр'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:66:in `блок в caches_action'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.
rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:189: в `вызове'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:638:in `заблокировать в run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:91:in `фильтр'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/caching/actions.rb:66:in `блок в caches_action'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/callbacks.rb:182:in `evaluate_method'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:184:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.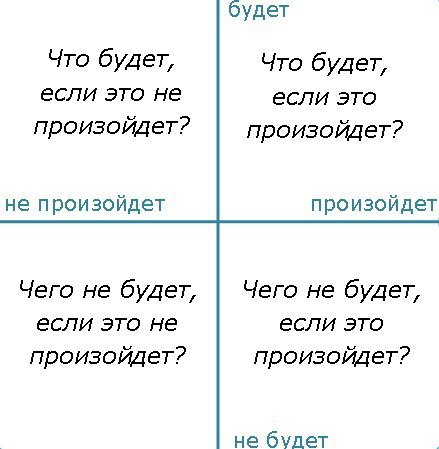 rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:610:in `perform_action_with_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `заблокировать в Perform_action_with_benchmark'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `блок в мс'
/usr/share/ruby/benchmark.rb:308:в `реальном времени'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `мс'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `perform_action_with_benchmark'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/rescue.rb:160:in `perform_action_with_rescue'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/flash.rb:151:in `perform_action_with_flash'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.
rb:635:in `run_before_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:615:in `call_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:610:in `perform_action_with_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `заблокировать в Perform_action_with_benchmark'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `блок в мс'
/usr/share/ruby/benchmark.rb:308:в `реальном времени'
/home/nlab/www/nlab/vendor/rails/activesupport/lib/active_support/core_ext/benchmark.rb:17:in `мс'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/benchmarking.rb:68:in `perform_action_with_benchmark'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/rescue.rb:160:in `perform_action_with_rescue'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/flash.rb:151:in `perform_action_with_flash'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base. rb:532:в `процессе'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:606:in `process_with_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:391: в `процессе'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:386:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/routing/route_set.rb:438:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:87:в `dispatch'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:121:in `_call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:130:in `блок в build_middleware_stack'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/string_coercion.rb:29: в `вызове'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/head.rb:12:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/method_override.rb:24:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/params_parser.
rb:532:в `процессе'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/filters.rb:606:in `process_with_filters'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:391: в `процессе'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/base.rb:386:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/routing/route_set.rb:438:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:87:в `dispatch'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:121:in `_call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:130:in `блок в build_middleware_stack'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/string_coercion.rb:29: в `вызове'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/head.rb:12:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/method_override.rb:24:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/params_parser. rb:15:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/metal.rb:47:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/session/abstract_store.rb:177:in `call'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:29:in `заблокировать вызов'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/query_cache.rb:34:в `кеше'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:9:в `кеше'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:28:in `call'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/connection_pool.rb:361:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/failsafe.rb:26:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/lock.rb:18:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:106:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/static.
rb:15:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/metal.rb:47:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/session/abstract_store.rb:177:in `call'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:29:in `заблокировать вызов'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/query_cache.rb:34:в `кеше'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:9:в `кеше'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/query_cache.rb:28:in `call'
/home/nlab/www/nlab/vendor/rails/activerecord/lib/active_record/connection_adapters/abstract/connection_pool.rb:361:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/failsafe.rb:26:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/rack-2.2.4/lib/rack/lock.rb:18:in `call'
/home/nlab/www/nlab/vendor/rails/actionpack/lib/action_controller/dispatcher.rb:106:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/static. rb:31:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/log_tailer.rb:17:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:634:in `process_client'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:739: в `worker_loop'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:547:in spawn_missing_workers
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:143:в `start'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/bin/unicorn_rails:209:in `
rb:31:in `call'
/home/nlab/www/nlab/vendor/rails/railties/lib/rails/rack/log_tailer.rb:17:in `call'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:634:in `process_client'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:739: в `worker_loop'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:547:in spawn_missing_workers
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/lib/unicorn/http_server.rb:143:в `start'
/home/nlab/www/nlab/vendor/bundle/ruby/3.0.0/gems/unicorn-6.1.0/bin/unicorn_rails:209:in ` 2.33/lib/bundler/cli/exec.rb:23:in `run'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:479: в `exec'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/command.rb:27:in `run'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/invocation.rb:127:in `invoke_command'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor.rb:392:in `dispatch'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:31:in `dispatch'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/base.rb:485:в `start'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:25:в `start'
/usr/share/gems/gems/bundler-2.2.33/libexec/bundle:49:in `заблокировать в
2.33/lib/bundler/cli/exec.rb:23:in `run'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:479: в `exec'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/command.rb:27:in `run'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/invocation.rb:127:in `invoke_command'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor.rb:392:in `dispatch'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:31:in `dispatch'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/vendor/thor/lib/thor/base.rb:485:в `start'
/usr/share/gems/gems/bundler-2.2.33/lib/bundler/cli.rb:25:в `start'
/usr/share/gems/gems/bundler-2.2.33/libexec/bundle:49:in `заблокировать в