1 6 сколько это в процентах: 1/6 Конвертер дробей и процентов, Дроби — kiteliberty.ru — Кайт клуб Андрея Антонова, Санкт-Петербург

Содержание

Калькулятор онлайн — Калькулятор процентов. Найти сколько процентов составляет одно число от другого

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или $ \frac{1}{100} $ часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р.

(сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы.

В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

$ 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 $

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

$ 0,58 = (0,58 \cdot 100)\% = 58\% $ $ 0,045 = (0,045 \cdot 100)\% = 4,5\% $

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.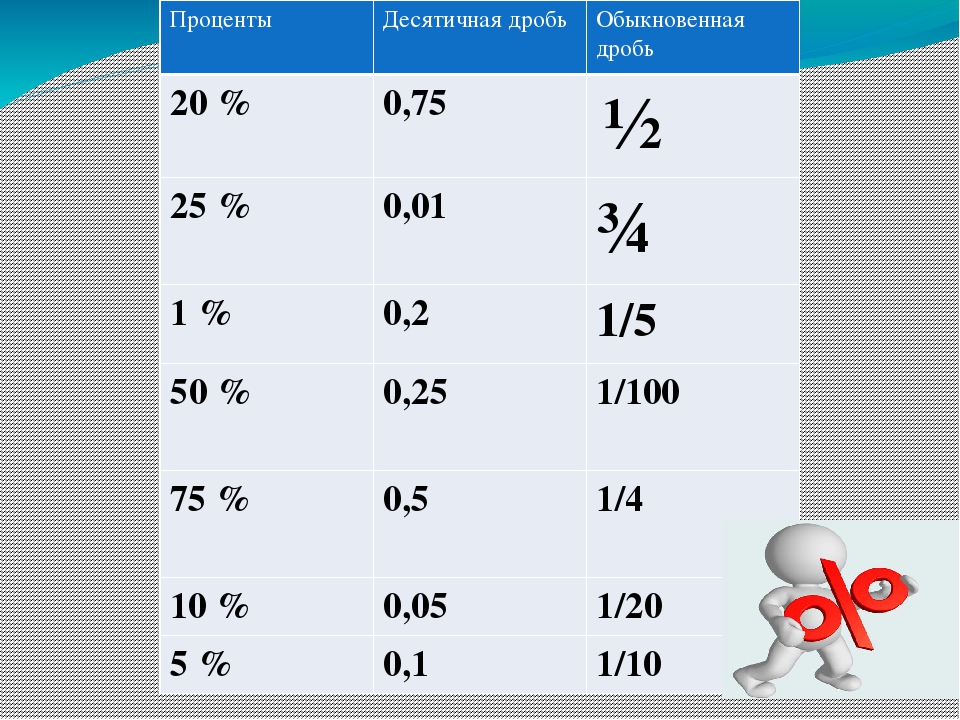

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти $ \frac{p}{100} $ от a, надо a умножить на $ \frac{p}{100} $:

$ b = a \cdot \frac{p}{100} $

Итак, чтобы найти р% от числа, надо это число умножить на дробь $ \frac{p}{100} $. Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью $ \frac{p}{100} , \; (p \neq 0) $, надо b разделить на $ \frac{p}{100} $:
$ a = b : \frac{p}{100} $

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на $ \frac{p}{100} $. Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а $ (a \neq 0) $, надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

$ p = \frac{b}{a} \cdot 100\% $ Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют $ \frac{9 \cdot 100}{180} = 5\% $ раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

$ b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) $ взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p.

Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или $ \frac{pn}{100}S $, а всего придется заплатить $ S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S $
Таким образом:
$ S_n = \left( 1+ \frac{pn}{100} \right) S $

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
$ S_n = \left( 1- \frac{pn}{100} \right) S $

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет

1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет $ \frac{p}{100}S $ р., и через год на счете окажется сумма
$ S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S $
то есть начальная сумма увеличится в $ 1+ \frac{p}{100} $ раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
$ S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S $

Аналогично $ S_3 = \left( 1+ \frac{p}{100} \right)^3 S $ и т. n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Калькулятор процентов • Популярные калькуляторы • Онлайн-конвертеры единиц измерения

Примеры решения задач на проценты

1. Расчет процента от числа

Найти число M, которое составляет P% от числа N.

В этом уравнении и в уравнениях ниже:

P% — процент, то есть число или отношение, выраженное в форме сотой части. В нашем примере P = 25%.

N — первое число (исходное число) , в нашем примере N = 150.

M — второе число, в нашем примере M = 37.5.

Пример: Сколько будет 25% от 150?

Результат: 25% от 150 равно 37.5.

2. Расчет процента увеличения или уменьшения, если известны исходное и новое значение

Какой процент P от N составляет число M? Иными словами, найти неизвестное число P, если известно, что P% от N равно M.

Пример: Какой процент от 200 составляет число 25?

Результат: 25 — это 12% от 200.

3. Расчет исходного числа по известному проценту от этого числа

Определить исходное число, если известно, что P% от этого числа равны M.

Пример: Определить исходное число, если известно, что 200% от этого числа равны 50. Иными словами, 50 — это 200% от какого числа?

Результат: 200% от 25 равны 50.

4. Расчет процентного увеличения (разницы в процентах между двумя числами)

Определить процент (P) увеличения исходного значения N, если известно, что после увеличения оно равно N.

Пример: На сколько процентов 200 больше 180?

Результат: 200 на 11,11% больше 180.

5. Расчет процентного уменьшения (разницы в процентах между двумя числами)

Определить процент (P) уменьшения исходного значения N, если известно, что после уменьшения оно равно N.

Другой пример: Магазин продавал товары по 20 евро за единицу. Продажа была не слишком успешной, поэтому для стимулирования продаж решили снизить стоимость до 15 евро. Определите убытки на единицу товара в процентном отношении к исходной цене.

Результат: Убытки на каждой единице товара с первоначальной стоимостью 20 евро и новой стоимостью 15 евро составили 25%.

6. Процентное увеличение числа

Определить число M, которое представляет собой P-процентное увеличение числа N.

Пример: Чему равно 10-процентное увеличение числа 5?

Результат: 10-процентное увеличение числа 5 равно 5,5.

7. Процентное уменьшение числа

Определить число M, которое представляет собой P-процентное уменьшение числа N.

Пример: Чему равно 10-процентное уменьшение числа 8?

Результат: 10-процентное уменьшение числа 8 равно 7,2.

Возможно, вас также заинтересует наш Калькулятор выделения и начисления НДС и налога с продаж.

Калькулятор процентов. Рассчитать процент от числа, вычислить отношение двух чисел.

Отношение чисел

Частное двух чисел называют отношением этих чисел.

Рассмотрим на примерах как находить отношение двух чисел.

Пример Найдем отношение чисел

4 и 20

Число 4 составляет 20% от числа 20. Для вычисления разделим 4 на 20 и умножим на 100, получим 4 &div; 20 × 100 = 20%

Число 20 составляет 500% от числа 4. Для вычисления разделим 20 на 4 и умножим на 100, получим 20 &div; 4 × 100 = 500%

Из числа 4 получим 20 увеличив на 400%. Для вычисления разделим 20 на 4, умножим на 100 и отнимем 100%, получим 20 &div; 4 × 100 — 100 = 400%

Из числа 20 получим 4 уменьшив число на 80%. Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 &div; 20 × 100 — 100 = -80%. Если в результате получается отрицательное значение, то число надо уменьшать, если положительно то увеличивать.

Найдем отношение двух вещественных чисел.

Пример Найдем отношение чисел

0.3 и 0.6

Число 0.3 составляет 50% от числа 0.6. Для вычисления разделим 0.3 на 0.6 и умножим на 100, получим 0.3 &div; 0.6 × 100 = 50%

Число 0.6 составляет 200% от числа 0.3. Для вычисления разделим 0. 6 на 0.3 и умножим на 100, получим 0.6 &div; 0.3 × 100 = 200%

Из числа 0.3 получим 0.6 увеличив на 100%. Для вычисления разделим 0.6 на 0.3, умножим на 100 и отнимем 100, получим 0.6 &div; 0.3 × 100 — 100 = 100%

Из числа 0.6 получим 0.3 уменьшив число на 50%. Для вычисления разделим 0.3 на 0.6, умножим на 100 и отнимем 100, получим 0.3 &div; 0. 6 × 100 — 100 = -50%.

Калькулятор процентов

Калькулятор процентов [an error occurred while processing the directive]

Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой

Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.

Калькулятор разработан специально для расчета процентов. Позволяет выполнять разнообразные расчеты при работе с процентами. Функционально состоит из 4-х разных калькуляторов. Примеры вычислений на калькуляторе процентов смотрите ниже.

Примеры вычислений на калькуляторе процентов

Какое число соответствует 23 % от числа 857 ?
Итог — 197. 11
Как вычислять:
Получаем коэффициент — 857 / 100% = 8.57.
Получаем итоговое число — 8.57 x 23% = 197.11

Сколько процентов составляет 24 от числа 248 ?
Итог — 9.677 %
Как вычислять:
Получаем коэффициент — 248 / 24 = 10.333
Получаем проценты — 100% / 10.333 = 9.677 %

Прибавить 35% к числу 487 ?
Итог — 657.45
Как вычислять:
Получаем коэффициент — 487 / 100 = 4.87
Получаем число равное 35% — 4.87 x 35 = 170.45
Получаем итоговое число — 170.45 + 487 = 657.45

Вычесть 17% из числа 229 ?
Итог — 190.07
Как вычислять:
Получаем коэффициент — 229 / 100 = 2. 29
Получаем число равное 17% — 2.29 x 17 = 38.93
Получаем итоговое число — 229 — 38.93 = 190.07

Процент, Процентное соотношение

Процент (что означает «на сотню») это сравнение с 100.

Символ процента %. Так, например, 5 процентов записывается как 5%.

Предположим, что в комнате 4 человека.

50% это половина — 2 человека.
25% это четверть — 1 человек.
0% это ничего — 0 человек.
100% это целое — все 4 человека в комнате.
Если в комнату заходят ещё 4 человека, то их колличество становится 200%.

1% это $\frac{1}{100}$
Если всего есть 100 человек, то 1% из них это один человек.

Чтобы выразить математически число X как процент от Y вы делаете следующее:
$X : Y \times 100 = \frac{X}{Y} \times 100$

Пример: Сколько процентов от 160 составляет 80?

Решение:

$\frac{80}{160} \times 100 = 50\%$

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.
Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) &div; Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) &div; Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$

Калькулятор Процентов

Как процентные соотношения помогают в реальной жизни

Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:

1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример: Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.

Решение:

Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:

(800 — 650) &div; 650 ⋅ 100 = 23,08%

Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.

Теперь давайте применим тоже самое ко второму месяцу:

(1200 — 800) &div; 800 ⋅ 100 = 50%

Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50&div;100=\$50). Теперь понятно,что доходы Тома растут.

2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример: Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.

Решение:

В табличке сказано, что

$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$

$Продано\ длина = \frac{60 \times 30}{100} = 18м$

Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.

Примеры:

1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?

Решение:

Общее количество карточек = 32 + 25 + 47 = 104

Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%

Процентное соотношение футбольных карточек = 25/104 x 100 = 24%

Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%

Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек.

2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

Решение:

Общее количество = 3×3 + 2×4 = 17 баллов

Полученные балы = 2×3 + 4 = 10 баллов

Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%

3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?

Решение:

Увеличение цены равно 40 x 20/100 = \$8

Новая цена равна 40 + 8 = \$48

Калькулятор Процентов и Как Рассчитать Проценты

Внимание! Пожалуйста, ждите, пока страница полностью не загружена, иначе калькулятор процентов не будет работать.

Примеры вычисления процента

Пример 1. Процент вычисления стоимости:

Что такое составляют 30% 70$?

30% разделены на 100 и умножены на 70$:

(30/100) x 70$ или 0.3 x 70$ = 21$

Пример 2. Формула для процента:

21$ что процент 70$?

21$ разделены на 70$ и умножены на 100:

($21/70) x 100 = 30%

Пример 3. Вычисление процентного изменения:

Процентное изменение между 50$ и 70$?

70 минус 50 разделили 50 умноженных на 100:

($ $70-50) / 50 x 100 или 0.4 x 100 = 40%

Пример 4. 15 процентов (%) 200:

Что составляет 15 процентов (%) 200

15% разделены на 100 и умножены на 200:

(15/100) x 200 или 0.15 x 200 = 30

Как вычислить процент с калькулятором процента онлайн.

Калькулятор процента – процент – любое отношение или число, разделенное на 100. Это обычно представляется знаком процента (%), или сокращением (процент). Буквальное значение процента за сотню, которая, очевидно, относится к числу, разделенному на 100.

Вычисления процента, вовлеченные в нахождение процентов, не очень трудные, и любой человек без большого ведома о математике может выполнить метод, чтобы получить результаты. Люди часто должны находить проценты, в некоторый момент в жизни.

Например, если Вы идете для покупок, и Вы хотите получить пару обуви, которая является в продаже, и Вы только должны заплатить 75% первоначальной цены, и первоначальная цена упомянута как 250$. Теперь, простое вычисление процента должно было бы разделиться 75 на 100 и затем умножить его к 250$. Теперь, Вы закончите тем, что получили 25% от цены.

В повседневной жизни Вы так или иначе, где-нибудь добрались бы, чтобы найти калькулятор использования или процент.

Студенты, учителя, бухгалтеры и много других профессий должны представлять числа как проценты. Выполнение процедуры вручную требует большого количества времени, и выполнение его приблизительно для приблизительно 100 количеств является действительно жесткой работой и вероятно заняло бы целый день, чтобы закончить.

В конце, после расходов такого количества драгоценных часов Ваших жизненных процентов нахождения, если бы ошибка найдена, который разрушил бы все следующие вычисления также, будет очень печалить. Это могло быть утомительно и очень, очень время, пропав впустую. Даже калькулятор не может сэкономить Ваше время.

Вы закончите тем, что скучали, расстроенные и усталые; кроме того, Вы не заставите время делать что-либо еще. Используйте Калькулятор Процента Онлайн!

В современном мире, когда все компьютеризировано и информационные технологии достигли своей высоты, где Вы можете получить почти что-нибудь перед Вами просто щелчком или два, почему бы не выбрать что-то более эффективное, экономящее время и безошибочное?

Вы знаете то, что я достигаю.

Да, почему бы не использовать калькулятор процента онлайн. Они более эффективны, меньше отнимающее много времени и гарантировали безошибочные калькуляторы. Все, в чем Вы нуждаетесь, является подключением к Интернету, и калькулятор процента находится в Вашей досягаемости.

Это действительно, большая помощь для учителей, которые должны вычислить проценты результата большого количества студентов для бухгалтеров, которые должны весь день иметь дело с процентами и некоторыми студентами, которые сталкиваются с трудностью в нахождении процентов.

Процесс, чтобы использовать алькулятор процента онлайн прост тогда, Вы вообразили бы.

Все, что Вы должны будете сделать, должно вставить стоимость, соответствующее пространство, и пресса входят, чтобы получить результаты. Эти калькуляторы предоставляют Вам наиболее удобный способ вычислить процент, уменьшая процент, увеличивая процент и другие ценности.

Калькулятор процента онлайн рекомендовал для использования в офисах, школе и почти любом месте, где Вы имеете Интернет в наличии.

Калькулятор процента может сэкономить Ваше время и позволить Вам получать самые точные результаты.

Как Посчитать Разницу В Процентах Между Двумя Числами

Как рассчитать проценты в MS Excel (video)

Напечатайте числа, и калькулятор процентов покажет Вам результат вычисления процента автоматически. Даже Вы будете видетьи как рассчитать проценты (формулу для того вычисления)!

Алименты на ребёнка в процентах от зарплаты

Кстати: Мы можем взыскать максимальные алименты Подробнее

Алименты, исчисляемые в процентном соотношении к заработной плате — стандартный способ выплаты, применяемый в большинстве случаев. Как правило, данная цифра берётся за основу даже при добровольной выплате содержания. Так как Семейным кодексом закреплено, что размер алиментов установленный соглашением сторон, не может быть ниже тех, которые полагаются ребёнку по закону. Однако часто можно услышать о том, что женщина получает с бывшего мужа на содержание ребёнка, например, лишь 1/10 его зарплаты и это вполне законно. А другой вовсе поступает не процент, а фиксированная сумма. Рассмотрим поподробнее, от чего зависит размер алиментов, выплачиваемых на детей.

Сколько процентов от зарплаты?

В 81 статье Семейного кодекса РФ закреплено долевое соотношение алиментов в зависимости от количества детей должника:

Если же плательщик имеет нерегулярный, меняющийся заработок, получает доход в иностранной валюте, алименты могут быть взысканы в твёрдой денежной сумме кратной величине прожиточного минимума.

В добровольно заключенном соглашении об уплате алиментов можно прописать и другие варианты выплат.

Какой процент от доходов родителя положен ребенку в виде алиментов после развода?

Если супруг уже выплачивает алименты?

Если предполагаемый должник уже имеет обязательства по выплате алиментов на содержание детей, это следует учитывать.

Например, Ирина хочет взыскать с бывшего мужа алименты на содержание их общего несовершеннолетнего ребёнка. Но бывший супруг уже выплачивает алименты на содержание ребёнка от первого брака. В этом случае Ирина может претендовать не на 1/4, а только на 1/6. Так как, на двоих детей взыскивается 1/3 дохода, следовательно, на каждого ребёнка по 1/6.

Но, если допустим, у вышеназванного должника появится ещё один ребёнок, на которого будут взыскиваться алименты, выплаты для первых двух детей не изменятся. Так как, если половину заработка разделить на троих — получается та же 1/6 от дохода. А вот при появлении четвёртого будет уже 1/8, в случае с пятым — 1/10.

При этом после достижения каждым из детей совершеннолетия, размер доли, удерживаемой из зарплаты должника, тоже же меняется. Например, как только двое из троих детей достигнут совершеннолетия, с должника будет удерживаться не 1/3, а 1/4 его заработной платы.

Важный для плательщиков алиментов нюанс заключается в том, что при появлении новых алиментных обязательств, размер доли, взысканной с них ранее, автоматически не изменяется. То есть, как только на второго ребёнка суд назначит выплату в размере 1/6, ранее установленная 1/4 от дохода на содержание первого ребёнка автоматически не изменится. Таким образом, будет удерживаться из зарплаты 1/4 на первого ребёнка и 1/6 на второго. У должника лишь появляется право обратиться в суд с иском об уменьшении размера алиментов в связи с появлением новых обязательств.

Как взыскать?

Если плательщик имеет постоянный доход и не выплачивает алименты другим детям, взыскать выплаты в долевом соотношении к заработку можно в судебном порядке, путём подачи заявления о вынесении судебного приказа. Обращаться следует в мировой суд по месту своего жительства (если с вами зарегистрированы дети) или посту жительства должника.

Заявление о выдаче судебного приказа о взыскании алиментов

Заявление будет рассмотрено судьёй в течение 5 дней без вызова сторон в судебное заседание. Судебный приказ о взыскании алиментов подлежит немедленному исполнению, его сразу же можно сдать в службу судебных приставов для принудительного взыскания.

Но должник имеет право его отменить.

Что делать в такой ситуации, читайте подробнее в статье: Судебный приказ на алименты

Судебный приказ о взыскании алиментов на ребенка

Если же алименты взыскиваются в фиксированной сумме, или плательщик уже выплачивает алименты другим детям — следует обращаться с исковым заявлением в районный суд.

Во всех нюансах процедуры взыскания алиментов поможет разобраться квалифицированный юрист. Специалист подскажет, какой из способов применительно к конкретной ситуации лучше выбрать, как взыскать алименты в большем размере или напротив уменьшить или изменить их величину. Доверив ведение дела специалисту, можете быть уверенными в том, что ребёнок получит максимально всё, причитающееся ему по закону и не будет ущемлён в своих правах.

Что такое 1/6 в процентах? (Преобразовать 1/6 в проценты)

При изучении дробей очень часто возникает вопрос, как преобразовать дробь, например, 1/6, в процент. В этом пошаговом руководстве мы покажем вам, как очень легко превратить любую дробь в процент. Давайте взглянем!

Хотите быстро научиться или показать студентам, как преобразовать 1/6 в процент? Воспроизведите это очень быстрое и веселое видео прямо сейчас!

Прежде чем мы начнем преобразование дроби в процент, давайте рассмотрим некоторые очень быстрые основы дроби.Помните, что числитель — это число над дробной чертой, а знаменатель — это число под дробной чертой. Мы будем использовать это позже в руководстве.

Когда мы используем проценты, на самом деле мы говорим, что процент — это доля от 100. «Процент» означает на сотню, и поэтому 50% — это то же самое, что сказать 50/100 или 5/10 в дробной форме.

Итак, поскольку наш знаменатель в 1/6 равен 6, мы можем скорректировать дробь, чтобы знаменатель стал равным 100.Для этого делим 100 на знаменатель:

100 ÷ 6 = 16,666666666667

Получив это, мы можем умножить числитель и знаменатель на это кратное:

1 х 16.666666666667 / 6 х 16.666666666667 знак равно 16.666666666667 / 100

Теперь мы видим, что наша доля составляет 16,666666666667 / 100, что означает, что 1/6 в процентах составляет 16,6667%.

Мы также можем решить это более простым способом, сначала преобразовав дробь 1/6 в десятичную. Для этого просто разделим числитель на знаменатель:

1/6 = 0.16666666666667

Получив ответ на это деление, мы можем умножить ответ на 100, чтобы получить процентное соотношение:

0,16666666666667 x 100 = 16,6667%

И вот оно! Два разных способа конвертировать 1/6 в процент. Оба варианта довольно просты и легки в выполнении, но я лично предпочитаю метод преобразования в десятичное число, поскольку он требует меньше шагов.

Я видел, как многие студенты путались, когда возникал вопрос о преобразовании дроби в проценты, но если вы выполните описанные здесь шаги, это должно быть просто.Тем не менее, вам все равно может понадобиться калькулятор для более сложных дробей (и вы всегда можете использовать наш калькулятор в форме ниже).

Если вы хотите попрактиковаться, возьмите ручку, блокнот и калькулятор и попробуйте самостоятельно преобразовать несколько дробей в проценты.

Надеюсь, это руководство помогло вам понять, как преобразовать дробь в процент. Теперь вы можете переходить и переводить дроби в проценты столько, сколько пожелает ваше маленькое сердце!

Калькулятор дробей в проценты

Доля в процентах

Введите числитель и знаменатель

Следующая дробь к вычислению процента

Доли в процентный калькулятор — Дюймовый калькулятор

Преобразуйте дробь в процент с помощью нашего калькулятора, указав свою дробь ниже.

Процент:

75%

Шаги для преобразования дроби в проценты

Найдите десятичную дробь, разделив числитель на знаменатель

34 = 3 ÷ 4 = 0,75

Найдите процент, умножив десятичную дробь на 100

0,75 × 100 = 75%

Вы хотите преобразовать процент в дробь?

Как преобразовать дробь в процент

Есть всего два простых шага, чтобы преобразовать дробь в процент.

Шаг первый: преобразование дроби в десятичное значение

Первый шаг — преобразовать дробь в десятичное значение. Сделайте это, разделив числитель на знаменатель.

В числителе указывается число над чертой дроби. Знаменатель — это число под чертой дроби.

десятичное число = числитель ÷ знаменатель

Например, преобразует дробь 34 в десятичную.

34 = 3 ÷ 4
34 = 0,75

Таким образом, десятичное значение 34 равно 0.75 .

Совет: вы можете использовать диаграмму десятичных эквивалентов для списка десятичных значений обычных дробей, чтобы преобразовать дробь в десятичную без использования деления.

Возможно, вас заинтересует наш калькулятор деления в столбик.

Шаг второй: преобразование десятичного значения в процентное значение

Второй шаг — преобразовать десятичное значение в проценты. Умножьте десятичное значение на 100 и поставьте после него знак процента (%).

Например, преобразует 0,75 в проценты.

процент = 0,75 × 100 = 75%

Таким образом, процентное значение 34 или 0,75 составляет 75% .

Таблица преобразования дробей в проценты

Другой способ преобразовать дробь в проценты — использовать таблицу преобразования. В приведенной ниже таблице преобразования показаны некоторые общие дроби и их эквивалентные проценты.

Таблица преобразования дробей в проценты, показывающая обычные дроби и их эквивалентные процентные значения.
Дробь	процентов
1/2	50%
1/3	33,3%
2/3	66,6%
1/4	25%
3/4	75%
1/5	20%
2/5	40%
3/5	60%
4/5	80%
1/6	16.66%
5/6	83,33%
1/8	12,5%
3/8	37,5%
5/8	62,5%
7/8	87,5%
1/9	11,1%
2/9	22,2%
4/9	44,4%
5/9	55,5%
7/9	77.7%
8/9	88,8%
1/10	10%
1/12	8,333%
1/16	6,25%

Смотрите больше эквивалентов долей в процентах.

Процентный калькулятор

Этот процентный калькулятор — инструмент, который позволяет вам делать простые вычисления: какой процент от X равен Y? Инструмент довольно прост. Все, что вам нужно сделать, это заполнить два поля, третье будет рассчитано автоматически.Этот метод позволит вам ответить на вопрос, как найти процентное соотношение двух чисел. Кроме того, наш процентный калькулятор также позволяет вам производить вычисления в обратном порядке, то есть как найти процент от числа. Попробуйте ввести различные значения в разные поля и посмотрите, насколько быстрый и простой в использовании этот удобный инструмент. Вам недостаточно только знать, как получить процент от числа? Если вам нужны более подробные вычисления, нажмите кнопку расширенного режима под калькулятором.

Помимо того, что этот инструмент полезен при изучении процентов и дробей, этот инструмент полезен во многих различных ситуациях. Вы можете найти проценты почти в по каждому аспекту вашей жизни! Любой, кто когда-либо был в торговом центре, наверняка видел десятки вывесок с большим символом процента, говорящим «Скидка ! ». И это только один из многих других примеров процентов. Они часто появляются, например, в финансах, где мы использовали их для определения суммы подоходного налога или налога с продаж, или в сфере здравоохранения, чтобы выразить, какой у вас жир.Продолжайте читать, если вы хотите узнать, как найти процентное соотношение чего-либо, какова процентная формула и как использовать проценты в других областях жизни, таких как статистика или физика.

Вот несколько калькуляторов для решения связанных проблем:

Какой процент? — Как узнать процент чего-либо?

Процент — это один из многих способов выразить безразмерное отношение двух чисел. Он очень популярен, поскольку может описывать ситуации, в которых участвует большое количество людей (например,g., оценивая шансы на выигрыш в лотерею), средние (например, определение итоговой оценки вашего курса), а также очень маленькие (например, объемная доля NO₂ в воздухе, также часто выражаемая в PPM — частях на миллион).

Один процент — сотая. В качестве знака процента мы обычно используем%, но иногда его обозначают как pct . Это означает, что 5 процентов совпадает с 5% , 5 процентов , 0,05 , 5/100 или пяти сотых .Это так просто, и этот процентный калькулятор — инструмент, предназначенный для работы с десятичными дробями и процентами. Если вы ищете более сложные проблемы, попробуйте выяснить, как рассчитать процентное соотношение.

Это все хорошо, но мы обычно не используем проценты сами по себе. В основном, мы хотим ответить , насколько велико одно число по сравнению с другим числом? . Чтобы попытаться визуализировать это, представьте, что у нас есть что-то, что нравится всем, например, большая пачка печенья (или пончиков, или конфет, что вы предпочитаете 😉 — мы будем придерживаться куки).Попробуем найти ответ на вопрос, что такое 40% от 20 ? Это 40 сотых от 20, поэтому, если мы разделим 20 файлов cookie на 100 равных частей (удачи с этим!), 40 из этих частей составят 40% от 20 файлов cookie. Давайте посчитаем: 40/100 * 20 = 8 . Небольшой удобный совет: чтобы разделить на 100, просто переместите точку на два деления влево. В нашем расчете 40/100 * 20 можно было бы сделать как (40 * 20) / 100 (это то же самое). 40 * 20 это 800.Переместив точку в 800 на две цифры влево, вы получите 8,00, а когда вы избавитесь от всех ненужных нулей, вы получите 8 . В нашем калькуляторе введите 40 и 20 (так что «40% от 20» равно 8).

Как найти процентное соотношение двух чисел? — Печенье! 🍪

Процент — это также способ выразить отношение между двумя числами в виде дроби от 100 . Другими словами, процент говорит нам, как одно число соотносится с другим. Если мы знаем, что число A составляет 25% от числа B , мы знаем, что A от до B похоже на 25 равно 100, или, после еще одного преобразования, например, от 1 до 4, т.е.е., A в четыре раза меньше, чем B . Это то, чему учит процентный калькулятор; что такое процент и как найти процентное соотношение двух чисел. Это необходимые и практические знания. Почему? Предположим, что B представляет собой массу человеческого тела или массу воздуха. Затем, обозначив A как массу воды, мы можем узнать, каков общий процент воды в организме или относительная влажность (используется для расчета точки росы воздуха).

Как найти процент на что-нибудь? Проще всего объяснить, какой процент у файлов cookie.Удивительно, как часто файлы cookie спасают положение, правда? Скажем, у нас есть большой ящик со 100 отделениями (сетка 10 x 10). Каждое отделение составляет сотую часть или 1% всего ящика. Затем мы заполняем этот ящик печеньем таким образом, чтобы в каждом отсеке было ровно файлов с одинаковым количеством файлов.

Сначала давайте начнем с самого простого примера: 100 файлов cookie . Как получить процент нескольких, скажем, пяти печенек? Это просто: в каждое отделение помещается ровно одно печенье.Итак, один процент от 100 — это один файл cookie , а пять процентов — это пять файлов cookie.

Давайте возьмем что-нибудь посложнее и в четыре раза вкуснее: 400 печенье ! Делим их поровну, и в каждом отделении по четыре печенья. Файлы cookie выглядят меньше, но в нашем воображении они такие же, только ящик намного больше! Один процент от 400 — это 4 . Как насчет 15 процентов? Это 15 отсеков по четыре печенья — 60 печенек. У нас начинают немного болеть животики, но это никогда не мешало нам есть больше печенья!

А теперь еще посложнее — 250 печенье .Ой-ой, мы разделили первые 200 печенек, положив по два в каждое отделение. Теперь у нас осталось 50 печенек, которые нужно распределить равномерно, хммм, по пол печенья в каждой коробке. Как рассчитать процент? Вы правы — на этот раз 1 процент от общего количества 250 файлов cookie составляет 2,5 . Сколько у нас в 15 коробках? 2,5 * 15 равно 37,5.

Так для чего нужен процент? Как мы писали ранее, процент — это способ выразить соотношение. Допустим, вы сдаете оценочный экзамен.Если бы мы сказали вам, что вы набрали 123 балла, это действительно ни о чем вам не скажет. 123 из чего? Теперь, если мы вам сказали, что вы получили 82% , эта цифра является более понятной информацией. Даже если бы мы вам сказали, вы получили 123 из 150; труднее почувствовать, насколько хорошо ты справился. Неделей ранее был еще один экзамен, и вы набрали 195 из 250, или 78%. Хотя сложно сравнить 128 из 150 и 195 из 250, легко сказать, что оценка 82% лучше, чем 78%. Разве знак процента не полезен? В конце концов, — это процент, который считается !

А как насчет десятичных дробей и процентов? Проценты можно легко преобразовать в десятичные числа. Просто разделите процент на 100, и все готово. 15% равно 0,15. Итак, как мы показали ранее, 0,15 из 250 файлов cookie — это тридцать семь с половиной.

Проценты иногда лучше выражают различные величины, чем десятичные дроби в химии или физике. Например, гораздо удобнее сказать, что процентная концентрация определенного вещества составляет 15,7%, чем 18,66 грамма вещества в 118,66 граммах раствора (как в примере в калькуляторе процентной концентрации).Другой пример — эффективность (или ее частный случай — эффективность Карно). Что лучше сказать, что автомобильный двигатель работает с КПД 20% или что он производит выходную энергию 0,2 кВтч из 1 кВтч энергии на входе? Как вы думаете? Мы уверены, что вы уже хорошо знаете, что умение получать процент от числа — это ценная способность.

Как найти процент от числа? — Другие примеры

Хотя использование нашего процентного калькулятора, безусловно, быстро и безболезненно, у вас не всегда есть доступ к компьютеру или смартфону.Кроме того, просто здорово иметь возможность производить вычисления в уме. Может быть, не так круто, как жонглирование пылающими факелами, но близко.

Процентное соотношение показывает, как число A соотносится с числом B . Пример из реальной жизни: в группе из пяти детей две девочки. Какой процент девушек? Другими словами, мы хотим знать, каково соотношение девочек ко всем детям. Это 2 из 5 или 2/5. Мы называем первое число (2) числителем , а второе число (5) знаменателем , потому что это дробь.Чтобы вычислить процент, умножьте эту дробь на 100 и добавьте знак процента. 100 * числитель / знаменатель = проценты . В нашем примере это 100 * 2/5 = 100 * 0,4 = 40 . Сорок процентов группы — девушки. Вот и вся процедура преобразования десятичных дробей в проценты. Говоря о десятичных дробях, есть способ кратко записывать очень большие или очень маленькие числа. Проверьте это с помощью нашего калькулятора научных обозначений!

У вас проблемы с упрощением дробей? Лучший способ решить эту проблему — найти GCF (наибольший общий коэффициент) числителя и знаменателя и разделить их на GCF.Вы можете найти здесь наш калькулятор GCF и LCM. Он ищет все множители обоих чисел, а затем показывает наибольшее общее. Как следует из названия, он также оценивает НОК, что означает наименьшее общее кратное.

Давайте обратимся и попробуем найти числитель . Допустим, мы знаем, что 70 процентов фруктов в корзине — яблоки, а всего 30 фруктов. Могло быть и хуже — это могли быть лимоны. Итак, сколько у нас яблок? Получим нашу процентную формулу: 100 * числитель / знаменатель = процент .Мы хотим узнать числитель. Давайте переместим все остальные части уравнения в другую сторону. Разделите обе части на 100 (чтобы избавиться от 100 слева), а затем умножьте обе части на знаменатель. Вот что мы получаем: числитель = процент * знаменатель / 100 . Заменим процент и знаменатель на наши значения: числитель = 70 * 30/100 . Теперь все просто: числитель = 2100/100 = 21 , у нас 21 яблоко. Должно хватить на обед или довольно жестокую кулинарную драку.

Теперь решим задачу с неизвестным знаменателем . Мы потратили 30 процентов своих карманных денег на жевательную резинку (мы никогда не говорили, что мы хорошие инвесторы). Мы купили 12 палочек по 1 доллару каждая. Итак, мы знаем, что 12 долларов составляли 30 процентов нашего общего бюджета. Сколько у нас было денег до того, как мы буквально все сдули? Начнем с нашей формулы: 100 * числитель / знаменатель = процентное соотношение или 100 * 12 / знаменатель = 30 . На этот раз мы хотим узнать знаменатель.Давайте умножим обе части на знаменатель, а затем разделим на процент. Таким образом, мы получим 100 * 12/30 = знаменатель . И наоборот, знаменатель = 100 * 12/30 = 1200/30 = 40 . У нас было 40 долларов, и мы потратили 30 процентов, или 12 долларов, на жевательную резинку. Оно того стоит.

Как рассчитать процент? Какая процентная формула?

Оставаясь с нашими примерами файлов cookie, давайте назовем три части в нашем уравнении: процентов, файлов cookie — 40%, , весь пакет, файлов cookie — 20 и часть , часть пакета файлов cookie — 8.В зависимости от того, что вы хотите оценить, вы можете написать три различных процентных формулы:

уравнение для процента следующее: процент = 100 * часть / целое , и оно отвечает на вопрос «какой процент от 20 равен 8».
формула для части: часть = целое * процентное соотношение / 100 , и она отвечает «что составляет 40% от 20?».
и, наконец, формула для целого: целое = 100 * часть / процент , и в ней говорится: «Что такое 100%, если 8 равно 40%?».

Это технически все. Теперь вы должны знать, как найти процент от числа.

Вы не поверите, но в спорте очень важно уметь считать проценты. Вы болеете за какую-нибудь спортивную команду? У нас есть для вас несколько интересных инструментов, которые включают проценты. Воспользуйтесь нашим калькулятором процента побед, чтобы узнать, насколько хорош прошлый сезон для вашей любимой команды. Кроме того, если вы планируете сделать ставку на свою команду (или сделать какие-либо другие инвестиции), посетите калькулятор рисков, чтобы узнать, какой вариант безопаснее.

История процента — знак процента

Хотя древние римляне использовали римские цифры I , V , X , L и т. Д., Вычисления часто выполнялись дробями, которые делились на 100. Это было эквивалентно вычислению процентов, которые мы знаем Cегодня. Вычисления со знаменателем 100 стали более стандартными после введения десятичной системы. Многие средневековые арифметические тексты применяли этот метод для описания финансов, например.г., процентные ставки. Однако знак процента%, который мы знаем сегодня, стал популярным лишь недавно, в 20-м веке, после многих лет постоянной эволюции.

Термин процент часто связывается с латинским % centum , что означает на сотню . На самом деле это неправильно. Мы получили термин из итальянского за сотку — за сотню . Знак процента% эволюционировал в результате постепенного сокращения этих слов на протяжении веков. В конце концов, cento принял форму двух окружностей, разделенных горизонтальной линией, от которой произошел современный символ%.История математических символов иногда поражает. Мы рекомендуем вам взглянуть на происхождение символа квадратного корня!

В последнее время символ процента широко используется в языках программирования в качестве оператора. Обычно это означает операцию по модулю. С другой стороны, в экспериментальной физике символ% имеет особое значение. Он используется для выражения относительной ошибки между истинным значением и наблюдаемым значением, обнаруженным в результате измерения.

Вы когда-нибудь встречали символ процента с дополнительным кружком? Это не ошибка! Есть два связанных знака:

‰ — промилле — промилле
‱ — за мириады — за десять тысяч (также известный как базисный пункт),

Далее по тексту мы более подробно объясним, что означает промилле, что такое базисный пункт и как преобразовать промилле и базисные пункты в проценты.

Для более высоких пропорций используются другие обозначения (называемые частями на миллион), например, доли на миллион (PPM), которые часто используются для измерения концентрации вещества в растворе или смеси. В настоящее время серьезную озабоченность вызывает смог — мельчайшие твердые частицы, которые попадают в воздух и могут серьезно повлиять на здоровье человека. Посетите наш калькулятор смога, чтобы узнать, сколько сигарет вы «выкуриваете», просто вдыхая воздух, и как вы можете противодействовать распространению загрязнений.

Орфография — проценты или проценты?

Процент или процент? Это зависит от вашей диеты.Если вы едите гамбургеры в большинстве приемов пищи, это процент. Если вы предпочитаете рыбу с жареным картофелем, это проценты. Если вы опрыскаете уксусом чипсы, пахнущие рыбой, то это будет процент, приятель (в отличие от процента любителей гамбургеров, чувак). Когда дело доходит до процентов, обе стороны пруда согласны: это должно быть одно слово. Все еще не понимаете? американцев говорят проценты, британцы используют проценты. Что-то подсказывает нам, что американский английский сейчас более популярен, поэтому на этом веб-сайте используется однословная форма.

После вкусного обеда самое время выпить чашечку кофе. Что общего между кофе и процентом, это может показаться вам довольно странным? Наш калькулятор кофе-пинка подскажет, какой у вас уровень бдительности в процентах в течение дня! Узнайте, как доза кофеина помогает вам оставаться сосредоточенным! Кроме того, если вы настоящий любитель кофе, попробуйте другие наши инструменты. С помощью калькулятора соотношения кофе и воды вы можете найти идеальное соотношение ингредиентов для приготовления чашки кофе, а калькулятор кофеина покажет вам, сколько кофеина вы выпили в течение дня.Имейте в виду, что вы также можете передозировать кофеин!

Что такое промилле? Что такое базисная точка?

промилле , промилле , промилле или просто ‰ аналогично проценту, только одна тысячная ( 1/1000 или 0,001 ). Если бюджет нашей семьи составляет 2400 долларов, и мы выделяем 1 промилле из него на покупку жевательной резинки, мы бы потратили 2,4 доллара (2 доллара 40 центов) на то, чтобы раздражать наших учителей (ну, 20 лет назад это было запрещено в польских школах.Сегодня мы не знаем правил 😃). Это очень похоже на то, как вы находите проценты. Если вы хотите использовать процентный калькулятор для подсчета промилле, просто используйте числа в 10 раз меньше (0,2 вместо 2, 4 вместо 40).

На бесчисленное множество , базисных точек или просто ‱ составляет одну десятитысячную ( 1/10000 или 0,0001 ). Это в 10 раз меньше промилле, поэтому для преобразования базисных пунктов в проценты необходимо разделить их на 100 .Это так просто!

Процентные пункты (процентные пункты)

Процентные точки (или процентные точки) — довольно хитрый зверь. Мы используем его все время, даже если мы этого не знаем — и в этих ситуациях мы часто неправильно говорим процент вместо процентного пункта . Прочитав этот раздел, вы будете знать, как это делать правильно, и будете раздражаться на всю оставшуюся жизнь (потому что другие люди будут продолжать совершать ошибки). Уже сейчас можно сказать, что процентные пункты играют важную роль в статистике, т.е.g., в нормальном распределении, биномиальном распределении или чтобы найти доверительный интервал для выборки данных (уровень достоверности обычно составляет 95 процентных пунктов).

Сенатор Гомер Симпсон в прошлом месяце набрал 10% голосов. С тех пор у него было несколько успешных дебатов, и теперь за него хотят проголосовать 12% населения. Что изменилось? Вы хотите сказать 2%, не так ли? Это не правильно! Давайте рассмотрим это. Представьте себе, что все население составляет 1000 человек. 10% из них — 100. 12% — 120. Каков процент увеличения? Это 100 * 20/100 = 20% !

Это ситуация, когда пригодятся процентные пункты.Мы используем процентные пункты, когда хотим говорить о переходе от одного процента к другому. Изменение с 10% до 12% составляет два процентных пункта (или 20 процентов).

Другой способ представить себе разницу в процентном изменении:

Изменение на процентных пунктов — это процентное изменение по отношению к предыдущему значению (10% в нашем примере и один процент от этого составляет одну сотую от 10% = 0,1%),
изменение в процентных пунктах относится ко всей части (целое — это вся генеральная совокупность или 1000 в нашем примере.1% из них 10). Чтобы рассчитать процентные пункты, просто вычтите один процент из другого . 30% на 20 процентных пунктов выше 10%. Указанный процентный пункт можно обозначить как стр.

Теперь, когда вы знаете все о процентных пунктах, мы гарантируем, что вы прочитаете или услышите, как другие люди неправильно говорят проценты, когда им следует использовать процентные точки. Если вы похожи на нас, вы будете кричать на газету, оскорбляя ее каким-то вымышленным языком.Эта реакция помогает освободить место вокруг вас, когда вы пользуетесь общественным транспортом 🙂

Калькулятор процентов

Укажите любые два значения ниже и нажмите кнопку «Рассчитать», чтобы получить третье значение.

Калькулятор процентов общими фразами

Калькулятор разницы в процентах

Калькулятор процентного изменения

Укажите любые два значения ниже и нажмите кнопку «Рассчитать», чтобы получить третье значение.

В математике процент — это число или отношение, представляющее долю от 100. Это часто обозначается символом «%» или просто как «процент» или «pct». Например, 35% эквивалентно десятичной дроби 0,35 или

Формула процента

Хотя процентную формулу можно записать в разных формах, по сути, это алгебраическое уравнение, включающее три значения.

P × V ₁ = V ₂

P — процентное значение, V ₁ — первое значение, которое будет изменено процентным соотношением, а V ₂ — результат процента, действующего на V ₁.Предоставленный калькулятор автоматически преобразует введенный процент в десятичное число для вычисления решения. Однако, если вычислить процентное значение, возвращаемое значение будет фактическим процентом, а не его десятичным представлением.

EX: P × 30 = 1,5

При решении вручную формула требует процентного значения в десятичной форме, поэтому решение для P необходимо умножить на 100, чтобы преобразовать его в процент. По сути, это то, что делает калькулятор выше, за исключением того, что он принимает значения в процентах, а не в десятичной форме.

Формула разницы в процентах

Процентная разница между двумя значениями рассчитывается путем деления абсолютного значения разницы между двумя числами на среднее значение этих двух чисел. Умножение результата на 100 даст решение в процентах, а не в десятичной форме. Обратитесь к уравнению ниже для пояснения.

Разница в процентах =

× 100

Формула процентного изменения

Увеличение и уменьшение в процентах рассчитывается путем вычисления разницы между двумя значениями и сравнения этой разницы с начальным значением.Математически это предполагает использование абсолютного значения разницы между двумя значениями и деление результата на начальное значение, по сути, вычисление того, насколько изменилось начальное значение.

Калькулятор процентного увеличения выше вычисляет увеличение или уменьшение определенного процента входного числа. Он в основном включает в себя преобразование процента в его десятичный эквивалент и либо вычитание (уменьшение), либо добавление (увеличение) десятичного эквивалента от и до 1, соответственно.Умножение исходного числа на это значение приведет либо к увеличению, либо к уменьшению числа на заданный процент. Обратитесь к примеру ниже для пояснения.

EX: 500 увеличен на 10% (0,1)
500 × (1 + 0,1) = 550

500 уменьшено на 10%
500 × (1 — 0,1) = 450

Калькулятор процентов | % эквивалент

Калькулятор процентов. Преобразование чисел между% процентов и математическими значениями полных или десятичных чисел.

Какой процент от нормального числа?

Введите значение:

Точность:

Полученные результаты: Сумма:

От единицы

Равно:

К единице

Выберите из единицы:

% percentdecimal #

Выберите «Кому»:

% percentdecimal #

Например, 75% эквивалентно десятичному числу 0,75 или ⁷⁵ ⁄ ₁₀₀ ≡ ¾ точным дробным числам.Такой простой, но очень точный инструмент может пригодиться, например, при разработке или расшифровке (продвинутой) формулы выпечки, где это на самом деле распространено. В математике мы используем процентные числа x% плюс дроби и десятичные дроби. С их помощью могут быть показаны одинаковые или разные математические значения, а также могут быть выполнены различные вычисления в процентах. Знак процента% можно сократить до трех букв pct . Используйте приведенную ниже таблицу для получения результатов математического преобразования.

Вычислить процентное соотношение между двумя числами

Математическая формула от десятичного числа к процентному результату —
Сначала умножьте десятичное число на число 100.Затем добавьте к результату символ «%». Учитесь на следующих соответствующих примерах.

0,3 десятичное число в процентах: 0,3 × 100 = 30%
0,85 десятичное число в процентах: 0,85 × 100 = 85%
1 десятичное число в процентах: 1 × 100 = 100%
6 десятичных чисел в процентах: 6 × 100 = 600%
15 десятичное число в процентах: 15 × 100 = 1,500%
33 десятичное число в процентах: 33 × 100 = 3,300%
33.333 десятичное число в процентах: 33,333 × 100 = 3 333,3%
77,5 десятичное число в процентах: 77,5 × 100 = 7,750%
100 десятичное число в процентах: 100 × 100 = 10 000%
125 десятичное число в процентах: 125 × 100 = 12500%

Математическая формула преобразования процента в десятичный результат —
Сначала разделите число в процентах на значение 100, затем удалите символ «%» из результата.Учитесь на примерах расчета от нескольких процентов до десятичных дробей.

0,7 процента в десятичном числе: 0,7% ÷ 100 = 0,007 десятичное число
1 процент в десятичной системе: 1% ÷ 100 = 0,01 десятичная дробь
5 процентов в десятичной системе: 5% ÷ 100 = 0,05 десятичная дробь
10 процентов в десятичном виде: 10% ÷ 100 = 0,1 десятичное число
25 процентов в десятичном виде: 25% ÷ 100 = 0,25 десятичное число
50 процентов до десятичного числа: 50% ÷ 100 = 0.5 десятичное
55 процентов в десятичном виде: 55% ÷ 100 = 0,55 десятичное
75 процентов в десятичном виде: 75% ÷ 100 = 0,75 десятичное
90 процентов в десятичном виде: 90% ÷ 100 = 0,9 десятичное число
95,3 процента в десятичном формате: 95,3% ÷ 100 = 0,953 десятичное число
99 процентов в десятичном виде: 99% ÷ 100 = 0,99 десятичное число
100 процентов в десятичном формате: 100% ÷ 100 = 1 десятичное число
120 процентов в десятичном формате: 120% ÷ 100 = 1.2 десятичное

Преобразование общих процентов в десятичные числа в дроби

9011 9011%0125 2%

диаграмма для: Процент преобразований
Процент равен	Десятичный № равен	Дробь равна
0,1%	0,001		0,00125	¹ ⁄ ₈₀₀
0.4%
1%	0,01	¹ ⁄ ₁₀₀
1,1%	0,011	¹¹ ⁄ _1,000
^12,5 ⁄ ₁₀₀₀
1,5%	0,015	³ ⁄ ₂₀₀
1,9%	0,019	0,019	1,9%	0,019	0,02	¹ ⁄ ₅₀
2,5%	0,025	¹ ⁄ ₄₀
3,33392
3,33392
5%	0.05	¹ ⁄ ₂₀
7,5%	0,075	³ ⁄ ₄₀
10%	0,19	9011			9011 12%	0,12	³ ⁄ ₂₅
12,5%	0,125	¹ ⁄ ₈
20%
20%
25%	0.25	¹ ⁄ ₄
30%	0,3	³ ⁄ ₁₀
33%	0,33			0,33	^{процентов}	десятичный #	дроби
33,33%	0,333	³³³ ⁄ ₁₀₀₀
40127 404	² ⁄ ₅
45%	0,45	⁹ ⁄ ₂₀
49%	0,49			0,49	9011 50%	0,5	¹ ⁄ ₂
55%	0,55	¹¹ ⁄ ₂₀
60%
65%	0.65	¹³ ⁄ ₂₀
66%	0,66	³³ ⁄ ₅₀
70%	0,7	9011	0,7	9011 75%	0,75	³ ⁄ ₄
80%	0,8	⁴ ⁄ ₅
82%
85%	0.85	¹⁷ ⁄ ₂₀
90%	0,9	⁹ ⁄ ₁₀
91%	0,91	9011	0,91	9011 95%	0,95	¹⁹ ⁄ ₂₀
99%	0,99	⁹⁹ ⁄ ₁₀₀
10092 1
процентов	десятичный #	дроби
101%	1.01	^{1 1} ⁄ ₁₀₀
110%	1,1	^{1 1} ⁄ ₁₀
125%	1,25		1,25			1,25
200%	2	² ⁄ ₁
300%	3	³ ⁄ ₁
1000 ₁
1,001%	10.01	^{10 1} ⁄ ₁₀₀
1,100%	11	¹¹ ⁄ ₁

Преобразовать дроби в проценты

Разделите верхнюю часть дроби на нижнюю, умножьте на 100 и добавьте знак «%».

Самый простой способ — использовать калькулятор

Шагов:

Разделите верхнюю часть дроби на нижнюю,
Затем умножьте результат на 100 и прочтите ответ!

Пример: Что такое

5 8 в процентах?

Возьмите калькулятор и введите «5 ÷ 8 =», калькулятор должен показать 0.625

Затем умножьте на 100 и получите ответ: 62,5%

(Не забудьте поставить знак «%», чтобы люди знали, что это «на 100»)

ИЛИ вы можете сначала умножить верхнюю на 100, а затем разделить на нижнее число:

Пример: Что такое

5 8 в процентах?

Сначала умножьте 5 на 100, затем разделите на 8

500 ÷ 8 = 62,5%

(Помните, что знак «%»!)

Или переместите десятичную запятую на 2 разряда

После деления вместо умножения на 100 мы можем просто переместить десятичную запятую на 2 разряда вправо , затем добавить%

Пример: преобразовать

¹/₈ в проценты

Разделить 1 на 8:

1 ÷ 8 = 0.125

Переместите десятичную точку на 2 позиции вправо

Не забудьте добавить знак «%»: 12,5%

Другой (более сложный) метод

Процент означает «на 100», поэтому попробуйте изменить дробь на ? 100 форма.

Выполните следующие действия:

Шаг 1. Найдите число, на которое можно умножить нижнюю часть дроби , чтобы получить 100.

Шаг 2: Умножьте верхнюю и нижнюю часть дроби на это число.

Шаг 3. Затем запишите только верхнее число со знаком «%».

Пример 1: преобразование

3 4 до процента

Шаг 1. Мы можем умножить 4 на 25 и получить 100

(почему 25? Потому что 100 делится на 4 равно 25)

Шаг 2: Умножьте верхнюю и нижнюю на 25:

× 25

3 4	=	75 100

× 25

Шаг 3: Запишите 75 со знаком процента:

Ответ = 75%

Пример 2: преобразование

3 16 до процента

Шаг 1: Нам нужно умножить 16 на 6.25, чтобы стать 100

(почему 6,25? Потому что 100 разделенное на 16 дает 6,25)

Шаг 2: Умножьте верхнюю и нижнюю на 6,25:

× 6,25

3 16	=	18,75 100

× 6.25

Шаг 3: Запишите 18,75 со знаком процента:

Ответ = 18,75%

Еще один метод: пропорции

Поскольку процент на самом деле является соотношением (частей на 100), мы также можем использовать Пропорции для преобразования.

Во-первых, запишите то, что вы знаете, в эту форму:

Верхняя часть фракции Нижняя часть фракции знак равно процентов 100

Затем решите, используя «умножить на известные углы, разделить на третье число» :

Пример: преобразование

3 16 до процентов

Впишите то, что вы знаете:

3 16 знак равно процентов 100

Умножьте на известные углы, затем разделите на третье число.»Известные углы»: верхний левый и нижний правый:

Процент = (3 × 100) / 16
= 300/16
= 18,75%

Ответ:

3 16 составляет 18,75% (тот же ответ, что и в предыдущем примере!)

Преобразование дробей в проценты

Помните, что процент — это просто особый способ выражения дроби как числа из 100 .

Чтобы преобразовать дробь в проценты, сначала разделите числитель на знаменатель.Затем умножьте десятичную дробь на 100 .

То есть дробь 4 8 может быть преобразован в десятичный разделив 4 от 8 . Его можно преобразовать в проценты, умножив десятичную дробь на 100 .

4 ÷ 8 знак равно 0,5 0,5 × 100 знак равно 50

Итак, дробь 4 8 эквивалентно 50 % .

Пример 1:

Писать 2 25 в процентах.

С 25 больше чем 2 , чтобы разделить, мы должны добавить десятичную точку и несколько нулей после 2 . Мы можем не знать, сколько нулей добавить, но это не имеет значения. Если мы добавим слишком много, мы сможем стереть лишнее; если мы не добавим достаточно, мы можем добавить еще.

Так,

2 25 знак равно 0.08 0,08 × 100 знак равно 8

Следовательно, дробь 2 25 эквивалентно 8 % .

Посмотрите на изображение ниже, оно показывает, что дробь 2 25 такой же как 8 снаружи 100 , это, 8 % .

Пример 2:

Писать 7 4 в процентах.

Делить 7 от 4 .

Так,

7 4 знак равно 1,75 1,75 × 100 знак равно 175

Следовательно, дробь 7 4 эквивалентно 175 % .

Пример 3:

Писать 1 8 в процентах.

Делить 1 от .

Так,

1 8 знак равно 0,125 0,125 × 100 знак равно 12,5

Следовательно, дробь 1 8 эквивалентно 12,5 % .