На порядок — это на сколько?
?
| ||||
| |||||||||||||||||||||||||||||||||
Честно.
..Порядок действий
В уроке выражения мы узнали, что они бывают числовые и буквенные.
Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.
Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто как 2 + 2 или 9 − 3.
Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.
Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:
Читаем выражение слева направо.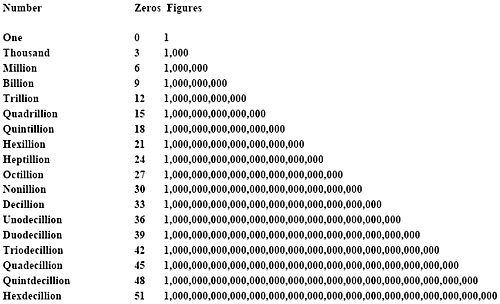
Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2.
Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:
Осталось простейшее выражение 11 + 3, которое вычисляется легко:
11 + 3 = 14
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
8 + 6 = 14Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением.
Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1.
Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
1) 3250 − 2905 = 345
2) 345 : 5 = 69
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799.
Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.
В результате будем иметь следующий порядок:
1) 6 411 × 8 = 51 288
2) 51 288 − 40 799 = 10 489
3) 10 489 × 6 = 62 934
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
1) 50 377 + 20 338 = 70 715
2) 1 657 974 : 822 = 2 017
3) 2 017 × 106 = 213 802
4) 213 802−70 715 = 143 087
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием.
При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
1) 96 : 4 = 24
2) 24 + 3 680 = 3 704
3) 14026 − 3 704 = 10 322
Задание 1. Найдите значение выражения:
5 + 2 − 2 − 1
Решение
Показать решение
Задание 2. Найдите значение выражения:
14 + (6 + 2 × 3) − 6
Решение
Показать решение
Задание 3. Найдите значение выражения:
486 : 9 − 288 : 9
Решение
Показать решение
Задание 4. Найдите значение выражения:
756 : 3 : 4 × 28
Решение
Показать решение
Задание 5. Найдите значение выражения:
807 : 3 − (500 − 58 × 4)
Решение
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Порядок величины — простая английская Википедия, бесплатная энциклопедия
Из простой английской Википедии, бесплатная энциклопедия
Порядок величины — это аппроксимация логарифма значения относительно некоторого контекстно понимаемого эталонного значения, обычно десяти, интерпретируется как основание логарифма и представитель значений величины один.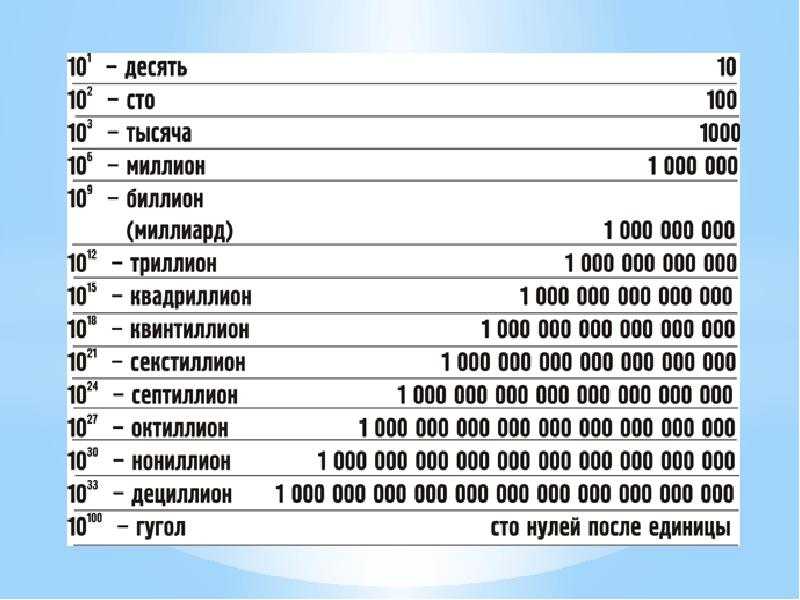
Логарифмические распределения широко распространены в природе.
рассмотрение порядка величины значений, выбранных из такого распределения, может быть более интуитивным. Когда эталонное значение равно десяти, порядок величины можно понимать как количество цифр в представлении значения по основанию 10. Точно так же, если эталонное значение является одной из определенных степеней двойки, величина может пониматься как объем компьютерной памяти, необходимый для хранения точного целочисленного значения.
Если два числа имеют одинаковый порядок величины , они примерно одного размера.
Но если сравнить поверхность апельсина с поверхностью земли, можно сказать, что поверхность земли на много порядков на больше, чем поверхность апельсина.
Порядки величин обычно используются для очень приблизительных сравнений. Он в основном используется при выполнении научных обозначений. Если два числа отличаются на один порядок, то одно примерно в десять раз больше другого.
Если они различаются на два порядка, то они различаются примерно в 100 раз. Два числа одного порядка имеют примерно одинаковый масштаб: большее значение меньше, чем в десять раз меньше меньшего.
| Полномочия из десяти | Порядка величины 1 | −100 1 | −93 |
|---|---|---|---|
| 0,000000000000000000000000000000000000000000000000000000000000000001 | −63 | ||
| 0,0000000000000000000000000000000001 | −33 | ||
| 0,0000000000000000000000000000001 | −30 | ||
| 0,0000000000000000000000000001 | −27 | ||
| 0,0000000000000000000000001 | −24 | ||
| 0,0000000000000000000001 | −21 | ||
| 0,000000000000000001 | −18 | ||
| 0,000000000000001 | −15 | ||
| 0,000000000001 | −12 | ||
| 0,00000000001 | −11 | ||
| 0,0000000001 | −10 | ||
| 0,000000001 | −9 | ||
| 0,00000001 | −8 | ||
| 0,0000001 | −7 | ||
| 0,000001 | −6 | ||
| 0,00001 | −5 | ||
| 0,0001 | −4 | ||
| 0,001 | −3 | ||
| 0,01 | −2 | ||
| 0,1 | −1 | ||
| 1 | 0 | ||
| 10 | 1 | ||
| 100 | 2 | ||
| 1000 | 3 | ||
| 10 000 | 4 | ||
| 100 000 | 5 | ||
| 1 000 000 | 6 | ||
| 10 000 000 | 7 | ||
| 100 000 000 | 8 | ||
| 1 000 000 000 | 9 | ||
| 10 000 000 000 | 10 | ||
| 100 000 000 000 | 11 | ||
| 1 000 000 000 000 | 12 | ||
| 1 000 000 000 000 000 | 15 | ||
| 1 000 000 000 000 000 000 | 18 | ||
| 1 000 000 000 000 000 000 000 | 21 | ||
| 1 000 000 000 000 000 000 000 000 | 24 | ||
| 1 000 000 000 000 000 000 000 000 000 | 27 | ||
| 1 000 000 000 000 000 000 000 000 000 000 | 30 | ||
| 1 000 000 000 000 000 000 000 000 000 000 000 | 33 | ||
| 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 63 | ||
| 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 93 | ||
| 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000, | 100 |
Для приблизительных сравнений используются порядки величин.
Если числа отличаются на один порядок, x — это примерно , в десять раз отличающееся по количеству от y . Если значения различаются на два порядка, они различаются примерно в 100 раз. Два числа одного порядка имеют примерно одинаковый масштаб: большее значение меньше, чем в десять раз меньше меньшего.
| Прописью (длинная шкала) | Прописью (короткая шкала) | Префикс (символ) | Десятичный | Сила из десяти | Порядка величины |
|---|---|---|---|---|---|
| дециллионная | ноябрядемиллионный | икосо- (и) | 0,00000000000000000000000000000000000000000000000000000000000001 | 10 −60 | −60 |
| немиллиардный | октадециллионная | эннеко- (е) | 0,0000000000000000000000000000000000000000000000000000000001 | 10 −57 | −57 |
| немиллионный | септендемиллионная | октеко- (о) | 0,0000000000000000000000000000000000000000000000000000001 | 10 −54 | −54 |
| октиллиард | сексдециллионный | гептеко- (л. с.) | 0,0000000000000000000000000000000000000000000000000001 | 10 −51 | −51 |
| октиллионный | пятимиллионный | гексеко- (hx) | 0,0000000000000000000000000000000000000000000000001 | 10 −48 | −48 |
| септмиллиард | quattuordecillionth | пентеко- (шт) | 0,0000000000000000000000000000000000000000000001 | 10 −45 | −45 |
| септиллионный | тредециллионная | тетреко- (трк) | 0,0000000000000000000000000000000000000000001 | 10 −42 | −42 |
| секстиллиарды | двенадцатиперстный | треко- (тк) | 0,00000000000000000000000000000000000000001 | 10 −39 | −39 |
| секстиллионная | ундециллионный | дуэко- (пост. ток) | 0,0000000000000000000000000000000000001 | 10 −36 | −36 |
| квинтиллиард | дециллионный | меко- (мк) | 0,0000000000000000000000000000000001 | 10 −33 | −33 |
| квинтиллионная | немиллионный | веко- (в) | 0,0000000000000000000000000000001 | 10 −30 | −30 |
| квадриллиард | октиллионный | ксоно- (х) | 0,0000000000000000000000000001 | 10 −27 | −27 |
| квадриллионный | септиллионный | йокто- (г) | 0,0000000000000000000000001 | 10 −24 | −24 |
| триллиард | секстиллионная | цепто- (г) | 0,000000000000000000001 | 10 −21 | −21 |
| триллионный | квинтиллионная | at- (а) | 0,000000000000000001 | 10 −18 | −18 |
| бильярдный | квадриллионный | фемто- (ф) | 0,000000000000001 | 10 −15 | −15 |
| миллиардный | триллионных | пико-(п) | 0,000000000001 | 10 −12 | −12 |
| миллиардные | миллиардный | нано- (н) | 0,000000001 | 10 −9 | −9 |
| миллионный | миллионный | микро- (мк) | 0,000001 | 10 −6 | −6 |
| тысячный | тысячный | милли-(м) | 0,001 | 10 −3 | −3 |
| сотый | сотый | санти- (с) | 0,01 | 10 −2 | −2 |
| десятый | десятый | деци- (д) | 0,1 | 10 −1 | −1 |
| один | один | 1 | 10 0 | 0 | |
| десять | десять | дека- (да) | 10 | 10 1 | 1 |
| сто | сот | гекто-(ч) | 100 | 10 2 | 2 |
| тысяч | тысяч | кило-(к) | 1000 | 10 3 | 3 |
| миллионов | миллионов | мега-(М) | 1000000 | 10 6 | 6 |
| миллиард | миллиардов | гига- (Г) | 1000000000 | 10 9 | 9 |
| миллиардов | триллионов | тера- (Т) | 1000000000000 | 10 12 | 12 |
| бильярд | квадриллион | пета- (П) | 1000000000000000 | 10 15 | 15 |
| трлн | квинтиллион | экса- (E) | 1000000000000000000 | 10 18 | 18 |
| триллиард | секстиллион | зетта- (З) | 1000000000000000000000 | 10 21 | 21 |
| квадриллион | септиллион | йотта- (Y) | 1000000000000000000000000 | 10 24 | 24 |
| квадрильярд | октиллион | ксенна- (X) | 1000000000000000000000000000 | 10 27 | 27 |
| квинтиллион | нониллионов | дака- (Да) | 1000000000000000000000000000000 | 10 30 | 30 |
| квинтиллион | дециллионов | хенда- (H) | 10000000000000000000000000000000000 | 10 33 | 33 |
| квинтиллион | ундециллионов | дока- (До) | 10000000000000000000000000000000000000 | 10 36 | 36 |
| квинтиллиард | дуодециллион | традака- (Td) | 10000000000000000000000000000000000000000 | 10 39 | 39 |
| секстиллион | тредециллион | тедака- (Тед) | 10000000000000000000000000000000000000000000 | 10 42 | 42 |
| секстильярд | кваттордециллион | педака- (Pd) | 10000000000000000000000000000000000000000000000 | 10 45 | 45 |
| септиллион | квиндециллион | exdaka- (Эд) | 10000000000000000000000000000000000000000000000000 | 10 48 | 48 |
| септиллиард | сексдециллион | зедака- (Zd) | 1000000000000000000000000000000000000000000000000000 | 10 51 | 51 |
| октиллион | септендециллион | йодака- (ярд) | 10000000000000000000000000000000000000000000000000000000 | 10 54 | 54 |
| октильярд | октодециллион | недака- (Nd) | 10000000000000000000000000000000000000000000000000000000000 | 10 57 | 57 |
| нониллионов | новемдециллион | ика- (ик) | 100000000000000000000000000000000000000000000000000000000000000 | 10 60 | 60 |
| Прописью (длинная шкала) | Прописью (короткая шкала) | Префикс (символ) | Десятичный | Сила из десяти | Порядка величины |
- Величина (математика)
- Степени 10, графическая анимированная иллюстрация, которая начинается с вида Млечного Пути на высоте 10 23 метров и заканчивается субатомными частицами на высоте 10 39 338 метров.
- Порядки величины — Расстояние
- Что такое порядок величины?
Что такое порядок величины?
К
- Бен Луткевич, Технический писатель
Порядок величины — это экспоненциальное изменение плюс или минус 1 значения величины или единицы. Этот термин обычно используется в сочетании с экспоненциальной записью степени 10.
Порядок величины используется, чтобы сделать размер чисел и измерений вещей более интуитивным и понятным. Обычно он используется для приблизительного сравнения двух чисел. Например, если окружность Солнца сравнить с окружностью Земли, окружность Солнца будет описана как на много порядков больше окружности Земли.
Как рассчитывается порядок величины? Порядок величины относится к классу шкалы любого числового значения, в котором каждый класс содержит значения фиксированного отношения к классу перед ним.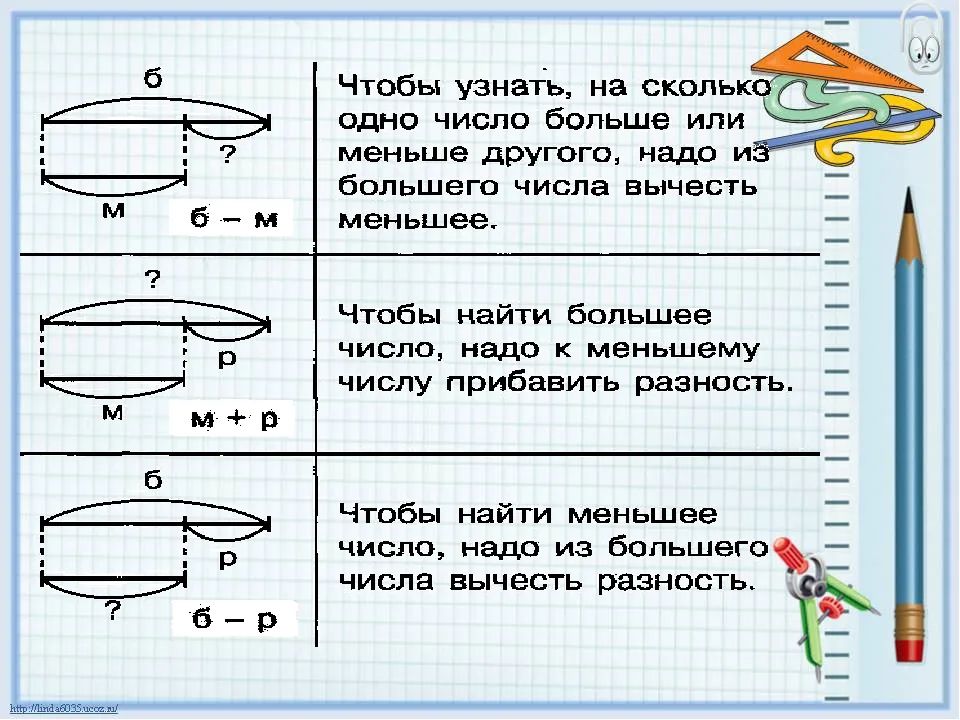
В логарифмической шкале, такой как основание 10, наиболее распространенная во всем мире схема счисления, увеличение на один порядок равносильно умножению количества на 10. Это увеличивает показатель степени на единицу до ближайшей степени 10. , Увеличение на два порядка эквивалентно умножению на 100, или 10 2 . В общем, увеличение n порядков эквивалентно умножению количества на 10 n . Таким образом, 2315 на один порядок больше, чем 231,5, что, в свою очередь, на один порядок больше, чем 23,15.
По мере уменьшения значений уменьшение на один порядок равносильно умножению количества на 0,1. Уменьшение на два порядка эквивалентно умножению на 0,01, или 10 -2 . В общем, уменьшение n порядков эквивалентно умножению количества на 10 -n . Таким образом, 23,15 на один порядок меньше, чем 231,5, что, в свою очередь, на один порядок меньше, чем 2315. По мере того, как порядок величины числа становится меньше, десятичная дробь смещается влево.
В Международной системе единиц большинство величин может быть выражено кратно или дробно в соответствии с порядком величины. Например, добавление префикса кило- к единице увеличивает размер единицы на три порядка, или на 1000 (10 3 ). Добавление префикса микро- к единице уменьшает размер единицы на шесть порядков, что эквивалентно умножению на 1 миллионную (10 -6 ). Ученые и инженеры обозначили префиксные множители от септиллионных долей (10 -24 ) до септиллионов (10 24 ), разброс в 48 порядков.
Хотя порядки величин не обязательно должны быть 10-кратными, обычно они таковы. Использование порядка величины и примерыПорядок величины используется для оценок и приблизительных сравнений в экспоненциальном представлении. Это способ представления чисел, которые сравнительно больше или меньше других чисел.
Некоторые примеры очень больших и очень малых чисел, которые выигрывают от представления по порядку величины, включают следующее:
- вес атома углерода
- размером с электрон
- длина тихоходки
- скорость суперкомпьютера
- возраст Земли
- количество данных в озере данных
- скорость флешки
Для выражения этих чисел используется научное обозначение.Некоторые различные способы использования этого порядка величины включают следующее:
Отличия. Это количество множителей 10, лежащих между двумя значениями. Например, если одно значение в 100 раз больше другого значения, первое значение на два порядка больше другого.
Оценки. Это когда порядок величины используется для оценки значения переменной с неизвестным точным значением. Например, если бы кто-то оценил население Земли, которое составляет около 7,9 миллиарда человек. Точное число неизвестно, но оно колеблется где-то между 1 и 10 миллиардами. Если округлить до следующего порядка, кто-то скажет, что население Земли составляет примерно 10 миллиардов, потому что оно кратно 10.
В Интернете есть бесплатные инструменты для расчета порядка величин. Эти инструменты используются для более простого и интуитивно понятного представления большего числа с использованием научных обозначений, например, количества эксабайтов в цифровом носителе данных.
Определение порядка величины также используется более свободно в различных контекстах. Этот термин может просто означать очень большое или малое число, большое или малое количество чего-либо или что-то значительно большее или меньшее.
Архитектура больших данных хранит огромные объемы данных, которые можно было бы использовать для измерения порядков величин. Изучите основные компоненты и рекомендации по созданию архитектуры больших данных, способной обрабатывать постоянно растущие объемы.
Последнее обновление: февраль 2022 г.
Продолжить чтение О порядке величины- ТБ и ГБ: терабайт больше гигабайта?
- Сколько байтов для . ..
..- Управление ростом данных в эпоху зетабайтов
- Как измерить производительность ИТ, шаг за шагом
- Nvidia SDK моделирует схемы квантовых вычислений на системах с GPU
словарь данных
Словарь данных — это набор описаний объектов данных или элементов модели данных, на которые могут ссылаться программисты и другие лица.
Сеть
- NFV MANO (управление и оркестрация виртуализации сетевых функций)
NFV MANO (управление виртуализацией и оркестровкой сетевых функций), также называемый MANO, представляет собой архитектурную основу для …
- Сетевой коммутатор
Сетевой коммутатор соединяет устройства в сети друг с другом, позволяя им общаться путем обмена пакетами данных.
- сетевой трафик
Сетевой трафик — это объем данных, которые перемещаются по сети в любое заданное время.
Безопасность
- контрольная сумма
Контрольная сумма — это значение, представляющее количество битов в передаваемом сообщении, которое используется ИТ-специалистами для обнаружения …
- информация о безопасности и управление событиями (SIEM)
Управление информацией о безопасности и событиями (SIEM) — это подход к управлению безопасностью, объединяющий информацию о безопасности …
- Злая Корпорация
Evil Corp — международная сеть киберпреступников, использующая вредоносное ПО для кражи денег с банковских счетов жертв и для …
ИТ-директор
- зеленые ИТ (зеленые информационные технологии)
Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислений.
- ориентир
Контрольный показатель — это стандарт или точка отсчета, которые люди могут использовать для измерения чего-либо еще.
- пространственные вычисления
Пространственные вычисления широко характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.
HRSoftware
- самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой …
- платформа обучения (LXP)
Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…
- Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
Отдел обслуживания клиентов
- прямой электронный маркетинг
Прямой маркетинг по электронной почте — это формат кампаний по электронной почте, в котором отдельные рекламные объявления рассылаются целевому списку .
